题目内容
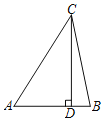
【题目】如图,P是直径AB上的一点,AB=6,CP⊥AB交半圆![]() 于点C,以BC为直角边构造等腰Rt△BCD,∠BCD=90°,连接OD.
于点C,以BC为直角边构造等腰Rt△BCD,∠BCD=90°,连接OD.

小明根据学习函数的经验,对线段AP,BC,OD的长度之间的关系进行了探究.
下面是小明的探究过程,请补充完整:
(1)对于点P在AB上的不同位置,画图、测量,得到了线段AP,BC,OD的长度的几组值,如下表:
位置1 | 位置2 | 位置3 | 位置4 | 位置5 | 位置6 | 位置… | |
AP | 0.00 | 1.00 | 2.00 | 3.00 | 4.00 | 5.00 | … |
BC | 6.00 | 5.48 | 4.90 | 4.24 | 3.46 | 2.45 | … |
OD | 6.71 | 7.24 | 7.07 | 6.71 | 6.16 | 5.33 | … |
在AP,BC,OD的长度这三个量中,确定________的长度是自变量,________的长度和________的长度都是这个自变量的函数;
(2)在同一平面直角坐标系xOy中,画出(1)中所确定的函数的图象;

(3)结合函数图象,解决问题:当OD=2BC时,线段AP的长度约为________.
【答案】(1)AP,BC,OD或BC,AP,OD;(2)如图1或图2所示:见解析;(3)线段AP的长度约为4.5.
【解析】
(1)由函数的自变量及函数的定义即可得出答案;
(2)利用描点法画出图象即可.
(3)由数形结合的思想,直接观察图象,由x=4.5时所对应的两个函数值即可发现此时OD=2BC.
(1) 由表格可确定BC随着AP的变化而变化,BD随着BC的变化而变化,故AP、BC的长度是自变量,OD或BC的长度和AP,OD的长度都是这个自变量的函数;
故答案为:AP,BC,OD或BC,AP,OD;在AP,BC,OD
(2)如图1或图2所示:
|
|
图1 | 图2 |
(3)由表格可知:当AP=4时,BC=3.46,OD=6.16; 当AP=4时,BC=2.45,OD=5.33,
∴当OD=2BC时
由可知线段AP的长度约为4.5.
|
|
图3 | 图4 |

【题目】现今“微信运动”被越来越多的人关注和喜爱,某数学兴趣小组随机调查了我市![]() 名教师某日“微信运动”中的步数情况进行统计整理,绘制了如下的统计图表(不完整):
名教师某日“微信运动”中的步数情况进行统计整理,绘制了如下的统计图表(不完整):
步数 | 频数 | 频率 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

请根据以上信息,解答下列问题:
(1)写出![]() ,
,![]() ,
,![]() ,
,![]() 的值并补全频数分布直方图;
的值并补全频数分布直方图;
(2)我市约有![]() 名教师,用调查的样本数据估计日行走步数超过
名教师,用调查的样本数据估计日行走步数超过![]() 步(包含
步(包含![]() 步)的教师有多少名?
步)的教师有多少名?
(3)若在![]() 名被调查的教师中,选取日行走步数超过
名被调查的教师中,选取日行走步数超过![]() 步(包含
步(包含![]() 步)的两名教师与大家分享心得,用树形图或列表法求被选取的两名教师恰好都在
步)的两名教师与大家分享心得,用树形图或列表法求被选取的两名教师恰好都在![]() 步(包含
步(包含![]() 步)以上的概率.
步)以上的概率.