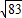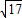题目内容
若a为方程（x-
）2=100的一根，b为方程（y-3）2=17的一根，且a、b都是正数，则a-b的值为（ ）
| 17 |
| A、13 | B、7 | C、-7 | D、-13 |
分析：根据题意，解出方程（x-
）2=100和（y-3）2=17的解，然后根据已知条件“且a、b都是正数”求得a、b的值，将其代入a-b并求值．
| 17 |
解答：解：由（x-
）2=100，得
x=±10+
，
∵a为方程（x-
）2=100的一根，且a、是正数，
∴a=10+
；
由（y-3）2=17，得
y=±
+3，
∵b为方程（y-3）2=17的一根，且b是正数，
∴b=
+3；
∴a-b=10+
-
-3=7；
故选B．
| 17 |
x=±10+
| 17 |
∵a为方程（x-
| 17 |
∴a=10+
| 17 |
由（y-3）2=17，得
y=±
| 17 |
∵b为方程（y-3）2=17的一根，且b是正数，
∴b=
| 17 |
∴a-b=10+
| 17 |
| 17 |
故选B．
点评：本题考查了一元二次方程的解．本题逆用一元二次方程解的定义易得出a、b的值，因此在解题时要重视解题思路的逆向分析．
练习册系列答案
相关题目
若a为方程（x-
）2=100的一根，b为方程式（y-4）2=17的一根，且a、b都是正数，则a-b之值为（ ）
| 17 |
| A、5 | ||
| B、6 | ||
C、
| ||
D、10-
|
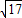）2=100的一根，b为方程式（y-4）2=17的一根，且a、b都是正数，则a-b之值为（ ）
