题目内容
【题目】解答题
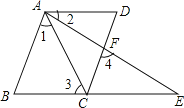
(1)如图1,AD、BC相交于点O,OA=OC,∠OBD=∠ODB.求证:AB=CD. 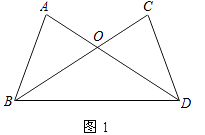
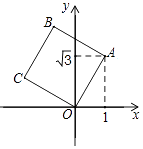
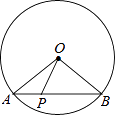
(2)如图2,AB是⊙O的直径,OA=1,AC是⊙O的弦,过点C的切线交AB的延长线于点D,若OD= ![]() ,求∠BAC的度数.
,求∠BAC的度数. 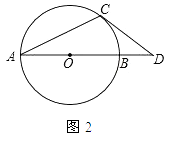
【答案】
(1)证明:∵∠OBD=∠ODB,
∴OB=OD,
在△AOB与△COD中, 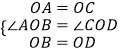 ,
,
∴△AOB≌△COD(SAS),
∴AB=CD
(2)解:连接OC,如图所示:

∵CD与⊙O相切,
∴OC⊥CD,
∵OA=OC,OA=1,
∴OC=1,
∴CD= ![]() =
= ![]() =1,
=1,
∴CD=OC,
∴△OCD为等腰直角三角形,
∴∠COB=45°,
∴∠BAC= ![]() ∠COB=22.5°.
∠COB=22.5°.
【解析】(1)由∠OBD=∠ODB,得出OB=OD,再由SAS证得△AOB≌△COD,即可得出结论;(2)连接OC,由CD与⊙O相切,得出OC⊥CD,求出CD=1,得出△OCD为等腰直角三角形,推出∠COD=45°,即可得出结果.
【考点精析】认真审题,首先需要了解切线的性质定理(切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径).

练习册系列答案
 综合自测系列答案
综合自测系列答案
相关题目