题目内容
在等腰梯形ABCD中,AD∥BC,AB=DC,且BC=2.以CD为直径作⊙O1交AD于点E,过点E作EF⊥AB于点F.建立如图所示的平面直角坐标系,已知A、B两点坐标分别为A(2,0)、B(0,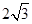 ).
).
【小题1】求C、D两点的坐标;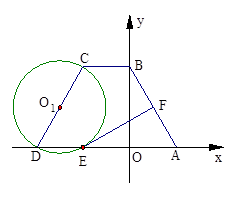
【小题2】求证:EF为⊙O1的切线
【小题3】线段CD上是否存在点P,使以点P为圆心,PD为半径的⊙P与y轴相切.如果存在,请求出P点坐标;如果不存在,请说明理由.
【小题1】连结CE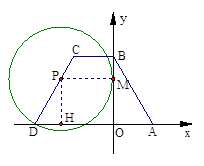
∵CD是⊙O1的直径 ∴CE⊥x轴
∴在等腰梯形ABCD中,EO=BC=2,
CE=BO=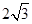 ,DE=AO=2∴DO=4,
,DE=AO=2∴DO=4,
故C(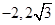 )D(
)D(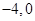 ) (3分)
) (3分)
【小题2】连结O1E,在⊙O1中,O1D= O1E,∠O1DE=∠1,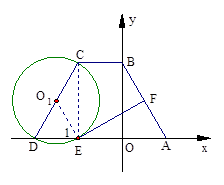
又在等腰梯形ABCD中 ∠CDA=∠BAD
∴∠1=∠BAD ∴O1E∥BA
又∵EF⊥BA ∴O1E⊥EF
∵E在⊙O1上 ∴EF为⊙O1的切线. (6分)
【小题3】存在满足条件的点P.
作PH⊥OD于H,作PM⊥y轴于M.
则当PM=PD时,⊙P于y轴相切.
在矩形PHOM中,OH=PM
设OH="m," 则PM="PD=m," DH=4-m
∵tan∠OAB=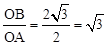
∴∠OAB=60°
∴∠PDH=∠OAB=60°
在Rt△PDH中,cos∠PDH=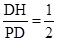 , 即:
, 即: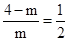 , m=
, m=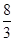 ,
,
则PH=DH·tan∠PDH="(4-m)" 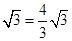
∴ 满足条件的P点坐标为(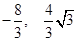 ) (12分)
) (12分)
解析

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
 25、如图所示,在等腰梯形ABCD中,AD∥BC,AB=CD,点P为BC边上任意一点,且
25、如图所示,在等腰梯形ABCD中,AD∥BC,AB=CD,点P为BC边上任意一点,且 24、已知:如图,在等腰梯形ABCD中,AD∥BC,AB=DC,点E为边BC上一点,且AE=DC.
24、已知:如图,在等腰梯形ABCD中,AD∥BC,AB=DC,点E为边BC上一点,且AE=DC.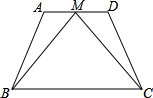 如图,在等腰梯形ABCD中,AD∥BC,M是AD的中点,MB=MC吗?为什么?
如图,在等腰梯形ABCD中,AD∥BC,M是AD的中点,MB=MC吗?为什么? 如图,在等腰梯形ABCD中,AD∥BC,AB=CD,AC⊥BD,垂足为O,过D作DE∥AC交BC的延长线于E.
如图,在等腰梯形ABCD中,AD∥BC,AB=CD,AC⊥BD,垂足为O,过D作DE∥AC交BC的延长线于E.