题目内容
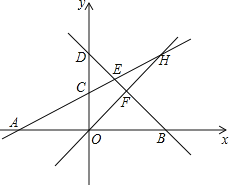
【题目】如图，直线AC：y＝
x+2分别交x轴和y轴于A，C两点，直线BD：y＝﹣x+b分别交x轴和y轴于B，D两点，直线AC与BD交于点E，且OA＝OB．
（1）求直线BD的解析式和E的坐标．
（2）若直线y＝x分别与直线AC，BD交于点H和F，求四边形ECOF的面积．
【答案】（1）y＝﹣x+4，点E坐标为（
，
）；（2）．
【解析】
（1）先求直线AC：y＝
x+2与x轴和y轴的交点A，C，由OA=OB得点坐标，代入直线BD：y=-x+b，求出b，即可知直线BD的解析式；再把直线BD的解析式与直线AC：y＝x+2联立即可求出点E的坐标．
（2）由（1）知点C，D，E的坐标，再联立y=x和直线BD的解析式，求出点F的坐标，由三角形DOF的面积减去三角形DCE的面积，即可求出四边形ECOF的面积．
解：（1）∵直线AC：y＝x+2分别交x轴和y轴于A，C两点，
∴A（﹣4，0），C（0，2），
∵OA＝OB，
∴OA＝OB＝4，B（4，0），
∵直线BD：y＝﹣x+b分别交x轴和y轴于B，D两点，
∴0＝﹣4+b，
∴b＝4，D（0，4）
∴直线BD：y＝﹣x+4．
解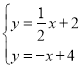
得 
∴
综上，直线 直线BD的解析式为：y＝﹣x+4，点E坐标为．
（2）由（1）知：C（0，2），D（0，4），E，
且由
，得点F（2，2），
∴S四边形ECOF＝S△DOF﹣S△DCE
＝4×2÷2﹣（4﹣2）×÷2
＝4﹣
＝
故四边形ECOF的面积为．
练习册系列答案
名师点拨卷系列答案
英才计划期末调研系列答案
相关题目
