题目内容
【题目】如图，A、B、C分别是线段A1B，B1C，C1A的中点，若△ABC的面积是1，那么△A1B1C1的面积 ． 
【答案】7
【解析】解：如图，连接AB1 ， BC1 ， CA1 ， ∵A、B分别是线段A1B，B1C的中点，
∴S△ABB1=S△ABC=1，
S△A1AB1=S△ABB1=1，
∴S△A1BB1=S△A1AB1+S△ABB1=1+1=2，
同理：S△B1CC1=2，S△A1AC1=2，
∴△A1B1C1的面积=S△A1BB1+S△B1CC1+S△A1AC1+S△ABC=2+2+2+1=7．
故答案为：7．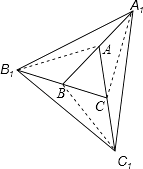
连接AB1 ， BC1 ， CA1 ， 根据等底等高的三角形的面积相等求出△ABB1 ， △A1AB1的面积，从而求出△A1BB1的面积，同理可求△B1CC1的面积，△A1AC1的面积，然后相加即可得解．
练习册系列答案
相关题目
