题目内容
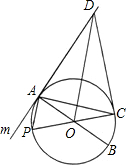 如图,已知⊙O的直径AB=2,直线m与⊙O相切于点A,P为⊙O上一动点(与点A、点B不重合),PO的延长线与⊙O相交于点C,过点C的切线与直线m相交于点D.
如图,已知⊙O的直径AB=2,直线m与⊙O相切于点A,P为⊙O上一动点(与点A、点B不重合),PO的延长线与⊙O相交于点C,过点C的切线与直线m相交于点D.(1)求证:△APC∽△COD;
(2)设AP=x,OD=y,试用含x的代数式表示y;
(3)试探索x为何值时,△ACD是一个等边三角形.
分析:(1)由题可知,DA、DC是由D点向圆引的两条切线,有切线的性质可知,DO垂直平分AC,又∠PAC为直径所对的圆周角为90°,所以PA和AC垂直,因此PA和OD平行,可得同位角相等即∠P=∠DOC,又∠PAC=∠DCO=90°,所以可得相似.
(2)由(1)知相似,可得对应线段成比例,利用此性质得
=
,可求出y与x之间的关系式.
(3)若△ACD是一个等边三角形,则∠ADC=60°,∠ODC=30°,于是OD=2OC,由(2)可得出x的值为1.
(2)由(1)知相似,可得对应线段成比例,利用此性质得
| AP |
| PC |
| OC |
| OD |
(3)若△ACD是一个等边三角形,则∠ADC=60°,∠ODC=30°,于是OD=2OC,由(2)可得出x的值为1.
解答:(1)证明:∵PC是⊙O的直径,CD是⊙O的切线,
∴∠PAC=∠OCD=90°,
∵DA,DC是⊙O的切线,
∴∠ADO=∠CDO,AD=DC,
∴DO⊥AC,
∴PA∥OD,
∴∠P=∠DOC,
∴△APC∽△COD.
(2)解:由△APC∽△COD,得:
=
∴
=
,
∴y=
.
(3)解:若△ACD是一个等边三角形,则∠ADC=60°,∠ODC=30°,
∵OD=2OC,
∴y=2,
∴x=1.
当x=1时,△ACD是一个等边三角形.
∴∠PAC=∠OCD=90°,

∵DA,DC是⊙O的切线,
∴∠ADO=∠CDO,AD=DC,
∴DO⊥AC,
∴PA∥OD,
∴∠P=∠DOC,
∴△APC∽△COD.
(2)解:由△APC∽△COD,得:
| AP |
| PC |
| OC |
| OD |
∴
| x |
| 2 |
| 1 |
| y |
∴y=
| 2 |
| x |
(3)解:若△ACD是一个等边三角形,则∠ADC=60°,∠ODC=30°,
∵OD=2OC,
∴y=2,
∴x=1.
当x=1时,△ACD是一个等边三角形.
点评:此题考查了相似三角形的判定以及切线长定理,难易程度适中.

练习册系列答案
相关题目
 2、如图,已知⊙O的直径AB⊥弦CD于点E,下列结论中一定正确的是( )
2、如图,已知⊙O的直径AB⊥弦CD于点E,下列结论中一定正确的是( )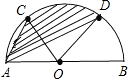 如图,已知半圆的直径AB=4cm,点C、D是这个半圆的三等分点,则弦AC、AD和
如图,已知半圆的直径AB=4cm,点C、D是这个半圆的三等分点,则弦AC、AD和
 22、如图,已知⊙O的直径为10,P为⊙O内一点,且OP=4,则过点P且长度小于6的弦共有
22、如图,已知⊙O的直径为10,P为⊙O内一点,且OP=4,则过点P且长度小于6的弦共有 如图,已知⊙O的直径AB与弦AC的夹角∠CAB=27°,过点C作⊙O的切线交AB延长线于点D,则∠ADC的度数为( )
如图,已知⊙O的直径AB与弦AC的夹角∠CAB=27°,过点C作⊙O的切线交AB延长线于点D,则∠ADC的度数为( ) (2010•邢台二模)如图,已知⊙O的直径AB与弦AC的夹角为31°,过C点的切线PC与AB的延长线交于点P,则∠P等于( )
(2010•邢台二模)如图,已知⊙O的直径AB与弦AC的夹角为31°,过C点的切线PC与AB的延长线交于点P,则∠P等于( )