题目内容
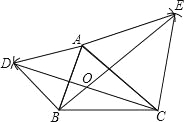
【题目】以AB、AC为边向△ABC外作等边△ABD和等边△ACE,连接BE,CD,请你完成图形,并证明:BE=CD.(尺规作图,不写作法,保留作图痕迹)
【答案】作图与证明见解析
【解析】
试题分析:分别以A、B为圆心,AB长为半径画弧,两弧交于点D,连接AD,BD,同理连接AE,CE,如图所示,由三角形ABD与三角形ACE都是等边三角形,得到三对边相等,两个角相等,都为60度,利用等式的性质得到夹角相等,利用SAS得到三角形CAD与三角形EAB全等,利用全等三角形的对应边相等即可得证.
试题解析:如图所示:
∵△ABD和△ACE都是等边三角形,
∴AD=AB,AC=AE,∠BAD=∠CAE=60°,
∴∠BAD+∠BAC=∠CAE+∠BAC,即∠CAD=∠EAB,
∵在△CAD和△EAB中,
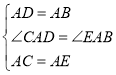 ,
,
∴△CAD≌△EAB(SAS),
∴BE=CD.

练习册系列答案
相关题目