题目内容
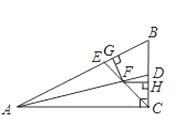
【题目】如图,在△ABC中,∠ACB是直角,∠B=60°,AD、CE分别是∠BAC、∠BCA的平分线,AD、CE相交于点F,且FG⊥AB于G,FH⊥BC于H.
(1)求证:∠BEC=∠ADC;
(2)请你判断并FE与FD之间的数量关系,并证明.
【答案】(1)证明见解析;(2)相等.
【解析】试题分析:(1)AD、CE分别是∠BAC、∠BCA的平分线,则可得∠DAC=∠DAB=15°
∠ACE= ∠ACB=45°,再由∠CDA=∠BAD+∠ABD,∠BEC=∠BAC+∠ECA,即可得;
(2)连接BF,根据角平分线的性质,可得FG=FH,又由在Rt△ABC中,∠ACB=90°,∠B=60°,求得∠GEF=75°=∠HDF,又由∠DHF=∠EHF=90°,利用AAS,即可证得△DHF≌△EGF,由全等三角形的对应边相等,即可证得FE=FD.
试题解析:(1)∵AD、CE分别是∠BAC、∠BCA的平分线,
∴∠DAC=∠DAB=![]() ∠BAC=15°
∠BAC=15°
∠ACE=![]() ∠ACB=45°,
∠ACB=45°,
∴∠CDA=∠BAD+∠ABD=75°,∠BEC=∠BAC+∠ECA=75°,
∴∠BEC=∠ADC;
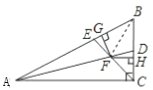
(2)相等,理由:如图,连接BF,
∵F是角平分线交点,
∴BF也是角平分线,
∴HF=FG,∠DHF=∠EGF=90°,
∵在Rt△ABC中,∠ACB=90°,∠ABC=60°,
∴∠BAC=30°,
∴∠DAC=12∠BAC=15°,
∴∠CDA=75°,
∵∠HFC=45°,∠HFG=120°,
∴∠GFE=15°,
∴∠GEF=75°=∠HDF,
在△DHF和△EGF中,
∠DHF=∠EGF,∠HDF=∠GEF,HF=GF,
∴△DHF≌△EGF(AAS),
∴FE=FD.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目



