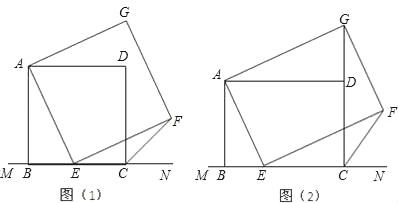
题目内容
【题目】E、F是线段AB上的两点,且AB=16,AE=1,BF=3,点G是线段EF上的一动点,分别以AG、BG为斜边在AB同侧作两个等腰直角三角形,直角顶点分别为D、C,如图所示,连接CD并取中点P,连结PG,点G从E点出发运动到F点,则线段PG扫过的图形面积为______.

【答案】36
【解析】
分别延长AD、BC相交于点H,连接PH,EH,FH,易证四边形DGCH为矩形,且P为矩形DGCH的对角线交点,即P为HG中点,过P作MN∥AB分别交EH、FH与M、N,所以MN为△HEF的中位线,即点P的运动轨迹即为MN,所以GP扫过的图形即为梯形MEFN,再根据已知线段求出梯形MEFN的面积即可.
解:分别延长AD、BC交于点H,连接PH,EH,FH,
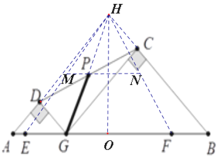
∵△ADG、△GCB为等腰直角三角形,
∴∠DGA=∠CGB=45°,
∴∠DGC=90°,
∴AH∥GC,
又∵∠HCG=90°,
∴∠HCG=∠DGC=90°,
∴DG∥HB,
∴四边形DGCH为矩形,
∵点P未DC中点,
∴点G、P、H三点共线,且P为HG的中点,
过P作MN∥于AB分别交EH、FH与M、N,
∴MN为△HEF的中位线,且MN即为点P的运动轨迹,
∴GP扫过的图形即为梯形MEFN,
∵AB=16,AE=1,BF=3,
∴EF=16-1-3=12,
∴![]() ,
,
过点H作HO垂直AB于O,
∴![]() ,
,
∴梯形的高为:![]() ,
,
∴![]() ,
,
即线段PG扫过的图形面积为36,
故答案为:36.

【题目】在一个不透明的盒子里装有只有颜色不同的黑、白两种球共50个,小颖做摸球实验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,下表是实验中的一组统计数据:
摸球的次数 | 100 | 200 | 300 | 500 | 800 | 1000 | 3000 |
摸到白球的次数 | 65 | 124 | 278 | 302 | 481 | 599 | 1803 |
摸到白球的频率 | 0.65 | 0.62 | 0.593 | 0.604 | 0.601 | 0.599 | 0.601 |
(1)请估计当![]() 很大时,摸到白球的频率将会接近 (精确到0.1);
很大时,摸到白球的频率将会接近 (精确到0.1);
(2)假如摸一次,摸到黑球的概率![]() ;
;
(3)试估算盒子里黑颜色的球有多少只.