题目内容
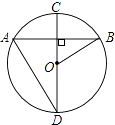
【题目】如图,在⊙O中,直径CD⊥弦AB,则下列结论中正确的是( ) 
A.AD=AB
B.∠BOC=2∠D
C.∠D+∠BOC=90°
D.∠D=∠B
【答案】B
【解析】解:A、根据垂径定理不能推出AD=AB,故A选项错误; B、∵直径CD⊥弦AB,
∴ ![]() =
= ![]() ,
,
∵ ![]() 对的圆周角是∠ADC,
对的圆周角是∠ADC, ![]() 对的圆心角是∠BOC,
对的圆心角是∠BOC,
∴∠BOC=2∠ADC,故B选项正确;
C、根据已知推出∠BOC=2∠ADC,不能推出3∠ADC=90°,故C选项错误;
D、根据已知不能推出∠DAB=∠BOC,不能推出∠D=∠B,故D选项错误;
故选:B.
【考点精析】利用垂径定理和圆周角定理对题目进行判断即可得到答案,需要熟知垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧;顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半.

练习册系列答案
相关题目
【题目】“3.15“植树节活动后,某校对栽下的甲、乙、丙、丁四个品种的树苗进行成活率观测,以下是根据观测数据制成的统计图表的一部分; 表1:栽下的各品种树苗棵数统计表表
植树品种 | 甲种 | 乙种 | 丙种 | 丁种 |
植树棵数 | 150 | 125 | 125 |
请你根据以上信息解答下列问题:
(1)这次栽下的四个品种的树苗共棵,乙品种树苗棵.
(2)图1中,甲%、乙%;
(3)已知这批树苗成活率为90%,将图2补充完整.