题目内容
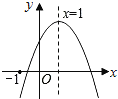
【题目】如图,己知抛物线y=k(x+1)(x﹣3k)(且k>0)与x轴分别交于A、B两点,A点在B点左边,与Y轴交于C点,连接BC,过A点作AE∥CB交抛物线于E点,0为坐标原点.
(1)用k表示点C的坐标(0, );
(2)若k=1,连接BE,
①求出点E的坐标;
②在x轴上找点P,使以P、B、C为顶点的三角形与△ABE相似,求出P点坐标;
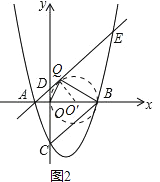
(3)若在直线AE上存在唯一的一点Q,连接OQ、BQ,使OQ⊥BQ,求k的值.
【答案】(1)﹣3k2;(2)①(4,5);②(![]() ,0)或(﹣
,0)或(﹣![]() ,0);(3)k=
,0);(3)k=![]() .
.
【解析】
试题分析:(1)只需把x=0代入抛物线的解析式,就可求出点C的坐标;
(2)①只需先求出直线AE的解析式,再求出直线AE与抛物线的交点坐标,就可解决问题;②由AE∥BC可得∠EAB=∠ABC,然后分△PBC∽△BAE和△PBC∽△EAB两种情况进行讨论,运用相似三角形的性质即可解决问题;
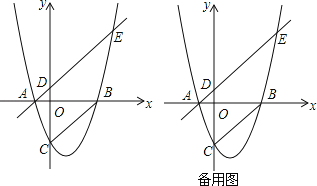
(3)由OQ⊥BQ可知点Q在以OB为直径的圆上,由于直线AE上存在唯一的一点Q,使得OQ⊥BQ,因此以OB为直径的圆与直线AE相切,切点为Q,圆心记为O′,连接O′Q,如图2,易证△AQO′∽△BOC,然后只需用k的代数式表示OC、QO′、AO′、BC,再运用相似三角形的性质就可求出k的值.
解:(1)当x=0时,y=k(0+1)(0﹣3k)=﹣3k2,
∴点C的坐标为(0,﹣3k2).
故答案为:﹣3k2;
(2)①∵k=1,
∴抛物线的解析式为y=(x+1)(x﹣3).
当x=0时,y=﹣3,则点C(0,﹣3),OC=3;
当y=0时,x1=﹣1,x2=3,
则点A(﹣1,0),点B(3,0),OA=1,OB=3.
∵AE∥CB,∴△AOD∽△BOC,
∴![]() =
=![]() ,
,
∴OD=1,即D(0,1).
设直线AE的解析式为y=kx+b,
则![]() ,
,
解得:![]() ,
,
∴直线AE的解析式为y=x+1,
联立![]() ,
,
解得:![]() 或
或![]() ,
,
∴点E的坐标为(4,5);
②过点E作EH⊥x轴于H,如图1,
则OH=4,BH=5,AH=5,AE=![]() =5
=5![]() .
.
∵AE∥BC,∴∠EAB=∠ABC.
Ⅰ.若△PBC∽△BAE,则![]() =
=![]() .
.
∵AB=4,BC=![]() =3
=3![]() ,AE=5
,AE=5![]() ,
,
∴![]() =
=![]() ,
,
∴BP=![]() ,
,
∴点P的坐标为(3﹣![]() ,0)即(
,0)即(![]() ,0);
,0);
Ⅱ.若△PBC∽△EAB,则![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴BP=![]() ,
,
∴点P的坐标为(3﹣![]() ,0)即(﹣
,0)即(﹣![]() ,0);
,0);
综上所述:满足条件的P点坐标为(![]() ,0)或(﹣
,0)或(﹣![]() ,0);
,0);
(3)∵直线AE上存在唯一的一点Q,使得OQ⊥BQ,
∴以OB为直径的圆与直线AE相切于点Q,圆心记为O′,连接O′Q,如图2,
则有O′Q⊥AE,O′Q=OO′=![]() OB.
OB.
当x=0时,y=k(0+1)(0﹣3k)=﹣3k2,则点C(0,﹣3k2),
当y=0时,k(x+1)(x﹣3k)=0,解得x1=﹣1,x2=3k,
则点A(﹣1,0),B(3k,0),
∴OB=3k,OA=1,OC=3k2,
∴O′Q=OO′=![]() ,O′A=
,O′A=![]() +1,BC=
+1,BC=![]() =3k
=3k![]() .
.
∵∠QAO′=∠OBC,∠AQO′=∠BOC=90°,
∴△AQO′∽△BOC,
∴![]() =
=![]() ,
,
∴QO′BC=AO′OC,
∴![]() 3k
3k![]() =(
=(![]() +1)3k2,
+1)3k2,
解得:k=![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案