题目内容
【题目】如图①，E在AB上，
、
都为等腰直角三角形，
，连接DB，以DE、DB为边作平行四边形DBFE，连接FC、DC．
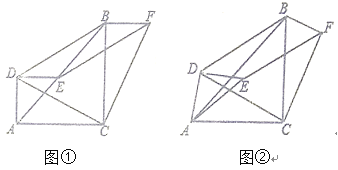
（1）求证：
；
；
（2）将图①中绕A点顺时针旋转，其它条件不变，如图②，（1）中的结论是否成立？说明理由．
（3）将图①中的绕A点顺时针旋转
，
，其它条件不变，当四边形DBFE为矩形时，直接写出
的值．
【答案】（1）见解析；（2）结论成立，见解析；（3）
或
【解析】
（1）先由△ACB、△ADE都为等腰直角三角形得出AD=DE，AC=BC，再由四边形DBFE是平行四边形得DE=BF，再证明∠CAD=∠CBF，即可证明△CAD≌△CBF，进而解决问题；
（2）延长DE交BC于M，只要证明△CAD≌△CBF即可解决问题；
（3）分两种情形画出图形即可解决问题.
（1）证明：如图①中，
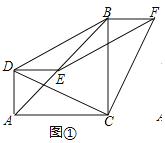
∵△ACB、△ADE都为等腰直角三角形，∠ADE=∠ACB=90°，
∴AD=DE，AC=BC，
∴∠AED=∠DAE=∠ABC=45°，
∵四边形DBFE是平行四边形，
∴DE=BF，DE∥BF，
∴AD=BF，∠FBE=∠DEB=180°-45°=135°，
∴∠FBC=135°-45°=90°，
∵∠CAD=∠CAB+∠DAE=45°+45°=90°，
∴∠CAD=∠CBF，
∴△CAD≌△CBF，
∴CD=CF，∠ACD=∠BCF，
∵∠ACD+∠BCD=90°
∴∠FCB+∠BCD=90°
∴∠DCF=∠ACB=90°，
∴CD⊥CF，CD=CF．
（2）结论成立．
理由：如图②中，延长DE交BC于M．
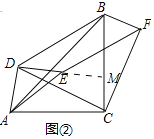
∵△ACB、△ADE都为等腰直角三角形，∠ADE=∠ACB=90°，
∴AD=DE，AC=BC，
∴∠AED=∠DAE=∠ABC=45°，
∵四边形DBFE是平行四边形，
∴DE=BF，DE∥BF，
∴∠FBC=∠DMB，
∵∠DAC+∠CMD=360°-90°-90°=180°，∠DMB+∠CMD=180°，
∴∠DAC=∠DMB，
∴∠FBC=∠CAD，
∴△CAD≌△CBF，
∴CD=CF，∠ACD=∠BCF，
∴∠DCF=∠ACB=90°，
∴CD⊥CF，CD=CF．
（3）如图③中，当旋转角α=45°时，四边形BDEF是矩形；
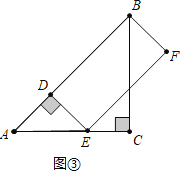
如图④中，当旋转角α=225°时，四边形BDEF是矩形；
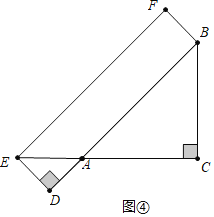
综上所述，α为45°或225°时，四边形EFBD是矩形．
