题目内容
正六边形ABCDEF内接于⊙O,⊙O的半径为6,则该正六边形的面积为________.
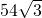
分析:由于正六边形可以分成六个边长的正三角形,而正多边形的半径即为正三角形的边长,所以首先求出正三角形的面积即可求出正六边形的面积,而正三角形的高可以利用解直角三角形解决问题.
解答:∵正六边形ABCDEF内接于⊙O,⊙O的半径为6,
而正六边形可以分成六个边长的正三角形,
∴正多边形的半径即为正三角形的边长,
∴正三角形的边长为6,
∴正三角形的高为6×sin60°=3
 ,
,∴该正六边形的面积为6×
 ×6×3
×6×3 =54
=54 .
.故答案为:54
 .
.点评:此题主要考查正多边形的计算问题,属于常规题,解题时分别利用三角形的面积公式、解直角三角形、勾股定理及垂径定理等知识.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
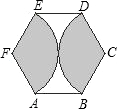 如图,正六边形ABCDEF的边长是3,分别以C、F为圆心,3为半径画弧,则图中阴影部分的面积是
如图,正六边形ABCDEF的边长是3,分别以C、F为圆心,3为半径画弧,则图中阴影部分的面积是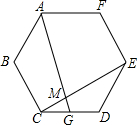 如图,G是正六边形ABCDEF的边CD的中点,连接AG交CE于点M,则GM:MA=
如图,G是正六边形ABCDEF的边CD的中点,连接AG交CE于点M,则GM:MA=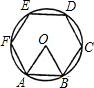 如图,⊙O的半径是6,求⊙O的内接正六边形ABCDEF的一边AB所对弧
如图,⊙O的半径是6,求⊙O的内接正六边形ABCDEF的一边AB所对弧
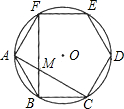 如图,圆内接正六边形ABCDEF中,AC、BF交于点M.则S△ABM:S△AFM=
如图,圆内接正六边形ABCDEF中,AC、BF交于点M.则S△ABM:S△AFM=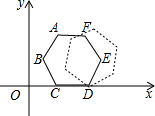 (2012•无锡)如图的平面直角坐标系中有一个正六边形ABCDEF,其中C、D的坐标分别为(1,0)和(2,0).若在无滑动的情况下,将这个六边形沿着x轴向右滚动,则在滚动过程中,这个六边形的顶点A、B、C、D、E、F中,会过点(45,2)的是点
(2012•无锡)如图的平面直角坐标系中有一个正六边形ABCDEF,其中C、D的坐标分别为(1,0)和(2,0).若在无滑动的情况下,将这个六边形沿着x轴向右滚动,则在滚动过程中,这个六边形的顶点A、B、C、D、E、F中,会过点(45,2)的是点