题目内容
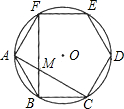 如图,圆内接正六边形ABCDEF中,AC、BF交于点M.则S△ABM:S△AFM=
如图,圆内接正六边形ABCDEF中,AC、BF交于点M.则S△ABM:S△AFM=分析:先根据正六边形的性质判断出△AMF≌△BMC,再求出△ABM与△AMF的高之比即可.
解答: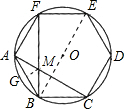 解:过M作MG⊥AB于G;
解:过M作MG⊥AB于G;
∵六边形ABCDEF是正六边形,
∴∠FAB=∠ABC=120°,AF=AB=BC,FE∥BC,FE=BC,
∴△ABF≌△ABC,∠AFM=∠ACB,
∴△AMF≌△BCM;
连接BE,
∵六边形ABCDEF是正六边形,
∴BE是⊙O的直径,∠MFE=∠MBC=90°,
∴∠FAM=90°,
∴S△ABM:S△AFM=GM:AM;
∵∠FAB=∠ABC=120°,∠FAM=90°,
∴∠MAB=∠BCM=30°,
∴
=sin30°=
,即S△ABM:S△AFM=
.
 解:过M作MG⊥AB于G;
解:过M作MG⊥AB于G;∵六边形ABCDEF是正六边形,
∴∠FAB=∠ABC=120°,AF=AB=BC,FE∥BC,FE=BC,
∴△ABF≌△ABC,∠AFM=∠ACB,
∴△AMF≌△BCM;
连接BE,
∵六边形ABCDEF是正六边形,
∴BE是⊙O的直径,∠MFE=∠MBC=90°,
∴∠FAM=90°,
∴S△ABM:S△AFM=GM:AM;
∵∠FAB=∠ABC=120°,∠FAM=90°,
∴∠MAB=∠BCM=30°,
∴
| GM |
| AM |
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查的是正六边形及等腰三角形的性质、圆周角定理,综合性较强,但难度适中.

练习册系列答案
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案
相关题目
 (1997•陕西)如图,圆内接正六边形ABCDEF中,AC,BF相交于点O,则S△ABO:S△AFO=
(1997•陕西)如图,圆内接正六边形ABCDEF中,AC,BF相交于点O,则S△ABO:S△AFO= 如图,圆内接正六边形ABCDEF中,AC,BF相交于点O,则S△ABO:S△AFO= .
如图,圆内接正六边形ABCDEF中,AC,BF相交于点O,则S△ABO:S△AFO= .
