题目内容
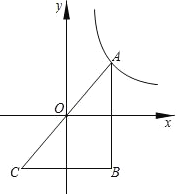
【题目】已知抛物线 y=![]() x2﹣2x的顶点是A,与x轴相交于点B、C两点(点B在点C的左侧).
x2﹣2x的顶点是A,与x轴相交于点B、C两点(点B在点C的左侧).
(1)求A、B、C的坐标;
(2)直接写出当y<0时x的取值范围.
【答案】(1)A的坐标是(2,﹣2),B的坐标是(0,0),C的坐标是(4,0);(2)x的范围是0<x<4.
【解析】
(1)利用配方法即可确定函数的顶点坐标;令y=0,解方程即可求得与x轴的交点的横坐标;
(2)y<0求x的范围,根据函数开口向上,以及函数与x轴的交点即可确定.
(1)y=![]() x2﹣2x=
x2﹣2x=![]() (x2﹣4x+4)﹣2=
(x2﹣4x+4)﹣2=![]() (x﹣2)2﹣2,
(x﹣2)2﹣2,
则函数的顶点坐标是(2,﹣2),
即A的坐标是(2,﹣2).
令y=0,则![]() x2﹣2x=0,
x2﹣2x=0,
解得x=0或4,
则B的坐标是(0,0),C的坐标是(4,0);
(2)x的范围是0<x<4.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目