��Ŀ����
����Ŀ���ۺ��⡣ 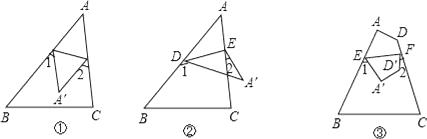
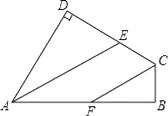
��1����ͼ�٣��ѡ�ABCֽƬ��DE�۵�������A�����ı���BCED�ڲ���A���λ��ʱ����A����1����2֮����������������ϵ����˵�����ɣ�
��2����ͼ�ڣ��ѡ�ABCֽƬ��DE�۵�������A�����ı���BCED�ⲿ��A���λ��ʱ����A����1����2֮����������������ϵ����˵�����ɣ�
��3����ͼ�ۣ����ı���ABCD��EF�۵�������A��D�ֱ������ı���BCFE�ڲ���A�䡢D���λ��ʱ�����������A�䡢��D�䡢��1 ���2֮���������ϵ�𣿲�˵�����ɣ�
���𰸡�
��1���⣺��ͼ�����ݷ��۵����ʣ���3= ![]() ����4=
����4= ![]() ��
��
�ߡ�A+��3+��4=180�㣬
���A+ ![]() +
+ ![]() =180�㣬
=180�㣬
�����ã�2��A=��1+��2
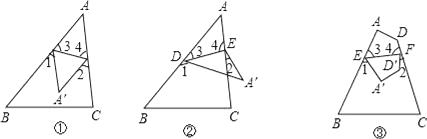
��2���⣺���ݷ��۵����ʣ���3= ![]() ����4=
����4= ![]() ��
��
�ߡ�A+��3+��4=180�㣬
���A+ ![]() =180�㣬
=180�㣬
�����ã�2��A=��1����2
��3���⣺���ݷ��۵����ʣ���3= ![]() ����4=
����4= ![]() ��
��
�ߡ�A+��D+��3+��4=360�㣬
���A+��D+ ![]() +
+ ![]() =360�㣬
=360�㣬
�����ã�2����A+��D��=��1+��2+360��
����������1�����ݷ��۵����ʱ�ʾ����3����4���ٸ��������ε��ڽǺͶ�����ʽ�������ɵý⣻��2���ȸ��ݷ��۵������Լ�ƽ�ǵĶ����ʾ����3����4���ٸ��������ε��ڽǺͶ�����ʽ�������ɵý⣻��3���ȸ��ݷ��۵����ʱ�ʾ����3����4���ٸ����ı��ε��ڽǺͶ�����ʽ�������ɵý⣮
�����㾫����������Ҫ�����������ε��ڽǺ���Ǻ������ε���ǵ����֪ʶ�㣬��Ҫ���������ε������ڽ��У�ֻ������һ���ڽ���ֱ�ǻ�۽ǣ�ֱ�������ε�������ǻ��ࣻ�����ε�һ����ǵ��ں��������ڵ������ڽǵĺͣ������ε�һ����Ǵ����κ�һ�����������ڵ��ڽǣ�������һ������һ�ߵ��ӳ�����ɵĽǣ��������ε���ǣ������ε�һ����ǵ��ں��������ڵ������ڽǵĺͣ������ε�һ����Ǵ����κ�һ�����������ڵ��ڽDz�����ȷ�����⣮

 ��У����ϵ�д�
��У����ϵ�д�����Ŀ��ij��˾10��ְ��5�·ݹ���ͳ�����£��ù�˾10��ְ��5�·ݹ��ʵ���������λ���ֱ��ǣ� ��
���ʣ�Ԫ�� | 2000 | 2200 | 2400 | 2600 |
�������ˣ� | 1 | 3 | 4 | 2 |
A.2400Ԫ��2400Ԫ
B.2400Ԫ��2300Ԫ
C.2200Ԫ��2200Ԫ
D.2200Ԫ��2300Ԫ