题目内容
【题目】如图,抛物线y=mx2﹣4mx+2m+1与x轴交于A(x1,0),B(x2,0)两点,与y轴交于点C,且x2﹣x1=2.
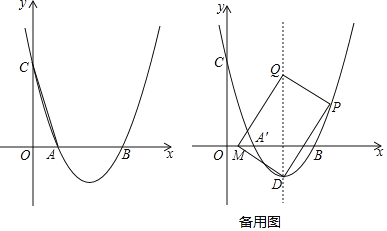
(1)求抛物线的解析式;
(2)E是抛物线上一点,∠EAB=2∠OCA,求点E的坐标;
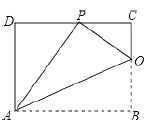
(3)设抛物线的顶点为D,动点P从点B出发,沿抛物线向上运动,连接PD,过点P做PQ⊥PD,交抛物线的对称轴于点Q,以QD为对角线作矩形PQMD,当点P运动至点(5,t)时,求线段DM扫过的图形面积.
【答案】(1)![]() ;(2)(
;(2)(![]() ,﹣
,﹣![]() )或(
)或(![]() ,
,![]() );(3)1.
);(3)1.
【解析】
(1)根据抛物线的对称轴公式以及与x轴的交点坐标可得![]() ,又x2﹣x1=2,可求得x1=1,x2=3,由此可得A,B两点坐标.将A点坐标代入抛物线解析式可求得m的值,由此可得抛物线解析式;
,又x2﹣x1=2,可求得x1=1,x2=3,由此可得A,B两点坐标.将A点坐标代入抛物线解析式可求得m的值,由此可得抛物线解析式;
(2)作MN垂直且平分线段AC,交y轴与点F,连接FA.可得∠OFA=2∠OCA,所以∠OFA=∠EAB,在Rt△OFA中表示∠OFA的正切值,分点E在x轴下方和x轴上方两种情况讨论,分别构造直角三角形表示∠EAB(∠E'AB)的正切值.根据相等角的正切值相等列出方程解方程即可;
(3)连接AD,过P作PS⊥QD于点S,作PH⊥x轴于点H,过B作BI∥QD,交PS于点I,先证明M的轨迹在x轴上,当P在B点时,M在A点.点P从点B出发沿抛物线向上运动时,M在A处沿x轴向左边运动.MD扫过的面积即S△MAD,求S△MAD即可.
解:(1)∵抛物线与x轴有两个交点A(x1,0),B(x2,0)
∴抛物线对称轴直线x=![]() =
=![]() =2
=2
∴![]()
又∵x2﹣x1=2
∴x1=1,x2=3
则点A(1,0),B(3,0)
把点A(1,0)代入y=mx2﹣4mx+2m+1中得,
m﹣4m+2m+1=0
解得,m=1
∴抛物线解析式为y=x2﹣4x+3
(2)如图①
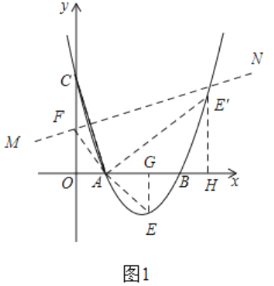
作MN垂直且平分线段AC,交y轴与点F.连接FA,则∠OFA=2∠OCA
由MN垂直平分AC得FC=FA,设F(0,n),则OF=n,OA=1
在Rt△OAF中,由勾股定理得,AF=![]() =
=![]()
∴FC=![]()
∴OC=OF+FC=n+![]() =3
=3
∴![]() =3﹣n
=3﹣n
等式左右两边同时平方得,1+n2=(3﹣n)2
解得,n=![]()
∴F(0,![]() )
)
∴tan∠OFA=![]() =
=![]() =
=![]()
①当抛物线上的点E在x轴下方时,作EG⊥x轴于点G,并使得∠EAB=∠OFA.
设点E(m,m2﹣4m+3),其中1<m<3,则tan∠EAB=![]() =
=![]() =
=![]()
整理得,4m2﹣13m+9=0
解得,m1=![]() ,m2=1(舍去)
,m2=1(舍去)
此时E点坐标为(![]() ,﹣
,﹣![]() );
);
②当抛物线上的点E'在x轴上方时,作E'H⊥x轴于点H,并使得∠E'AB=∠OFA.
设点E'(m,m2﹣4m+3),其中m>3,则tan∠E'AB=![]() =
=![]() =
=![]()
整理得,4m2﹣19m+15=0
解得,m3=![]() ,m4=1(舍去)
,m4=1(舍去)
此时E’点坐标为(![]() ,
,![]() )
)
综上所述,满足题意的点E的坐标可以为(![]() ,﹣
,﹣![]() )或(
)或(![]() ,
,![]() )
)
(3)如图②,
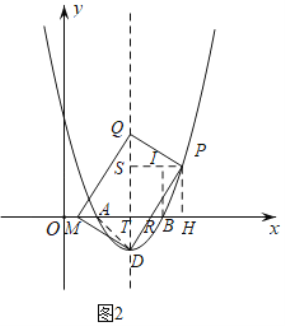
连接AD,过P作PS⊥QD于点S,作PH⊥x轴于点H,过B作BI∥QD,交PS于点I.
设QD⊥x轴于点T,DP与x轴交于点R.
∵在矩形PQMD中,MQ∥DP
∴∠QMH=∠MRD
又∵在△MDR中,∠MDR=90°
∴∠DMR+∠DRM=90°
又∵∠QMD=∠QMR+∠DMR=90°,R在x轴上
∴M恒在x轴上.
又∵PQ∥MD
∴∠PQS=∠MDT.
∴在△MTD与△PSQ中,
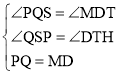
∴△MTD≌△PSQ(AAS)
∴MT=PS
又∵PS=TH
∴MT=TH
又∵AT=TB
∴MT﹣AT=TH﹣TB
即MA=BH.
又∵P点横坐标为5时,易得OH=5
∴BH=OH﹣OB=5﹣3=2
∴MA=2
又∵当P在B点时依题意作矩形PQMD,M在A点
由点P从点B由出发沿抛物线向上运动,易得M在A处沿x轴向左边运动.
∴MD扫过的面积即S△MAD
∴S△MAD=![]() MATD=
MATD=![]() ×2×1=1.
×2×1=1.
即线段DM扫过的图形面积为1.

 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案