题目内容
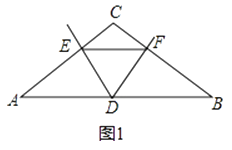
【题目】已知△ABC, ①如图1,若P点是∠ABC和∠ACB的角平分线的交点,则∠P=90°+ ![]() ∠A;
∠A;
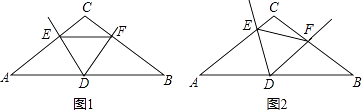
②如图2,若P点是∠ABC和外角∠ACE的角平分线的交点,则∠P=90°﹣∠A;
③如图3,若P点是外角∠CBF和∠BCE的角平分线的交点,则∠P=90°﹣ ![]() ∠A.
∠A.
上述说法正确的个数是( )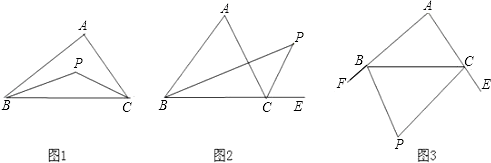
A.3个
B.2个
C.1个
D.0个
【答案】C
【解析】解:①若P点是∠ABC和∠ACB的角平分线的交点, 则∠PBC= ![]() ∠ABC,∠PCB=
∠ABC,∠PCB= ![]() ∠ACB
∠ACB
则∠PBC+∠PCB= ![]() (∠ABC+∠ACB)=
(∠ABC+∠ACB)= ![]() (180°﹣∠A)
(180°﹣∠A)
在△BCP中利用内角和定理得到:
∠P=180﹣(∠PBC+∠PCB)=180﹣ ![]() (180°﹣∠A)=90°+
(180°﹣∠A)=90°+ ![]() ∠A,
∠A,
故成立;
②当△ABC是等腰直角三角形,∠A=90°时,结论不成立;
③若P点是外角∠CBF和∠BCE的角平分线的交点,
则∠PBC= ![]() ∠FBC=
∠FBC= ![]() (180°﹣∠ABC)=90°﹣
(180°﹣∠ABC)=90°﹣ ![]() ∠ABC,
∠ABC,
∠BCP= ![]() ∠BCE=90°﹣
∠BCE=90°﹣ ![]() ∠ACB
∠ACB
∴∠PBC+∠BCP=180°﹣ ![]() (∠ABC+∠ACB)
(∠ABC+∠ACB)
又∵∠ABC+∠ACB=180°﹣∠A
∴∠PBC+∠BCP=90°+ ![]() ∠A,
∠A,
在△BCP中利用内角和定理得到:
∠P=180﹣(∠PBC+∠PCB)=180﹣ ![]() (180°+∠A)=90°﹣
(180°+∠A)=90°﹣ ![]() ∠A,
∠A,
故成立.
∴说法正确的个数是2个.
故选C.
【考点精析】本题主要考查了三角形的内角和外角和三角形的外角的相关知识点,需要掌握三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角;三角形一边与另一边的延长线组成的角,叫三角形的外角;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角才能正确解答此题.