题目内容
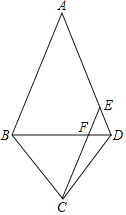
【题目】如图,△ABC中,AC=BC,∠BAC的外角平分线交BC的延长线于点D,若∠ADC=![]() ∠CAD,则∠ABC= 度.
∠CAD,则∠ABC= 度.

【答案】36
【解析】
设∠CDA=α,由∠ADC=![]() ∠CAD,根据角平分线定义得到∠CAD=∠DAE=2α,再根据三角形外角的性质得到∠B=2α﹣α=α,而AC=BC,得到∠BAC=∠B=α,然后根据三角形的内角和定理即可得到α.
∠CAD,根据角平分线定义得到∠CAD=∠DAE=2α,再根据三角形外角的性质得到∠B=2α﹣α=α,而AC=BC,得到∠BAC=∠B=α,然后根据三角形的内角和定理即可得到α.
解:设∠CDA=α,
∵∠ADC=![]() ∠CAD,
∠CAD,
∴∠CAD=2α,
而DA平分∠CAE,
∴∠CAD=∠DAE=2α,
而∠EAD=∠B+∠ADC,
∴∠B=2α﹣α=α,
又∵AC=BC,
∴∠BAC=∠B=α
在△ABD中,
∴∠B+∠CAB+∠CAD+∠ADC=180°,即α+α+2α+α=180°,
∴α=36°.
故答案为36.

练习册系列答案
相关题目