题目内容
【题目】如图,点B、C、E是同一直线上的三点,四边形ABCD与四边形CEFG都是正方形,连接BG、DE.
(1)求证:BG=DE;
(2)已知小正方形CEFG的边长为1cm,连接CF,如果将正方形CEFG绕点C逆时针旋转,当A、E两点之间的距离最小时,求线段CF所扫过的面积.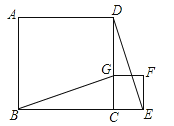
【答案】解:(1)∵四边形ABCD与四边形CEFG都是正方形,
∴BC=CD,CG=CE,∠BCG=∠DCE=90°,
在△BCG和△DCE中,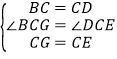 ,
,
∴△BCG≌△DCE,
∴BG=DE;
(2)由题意可知,当C、E、A三点在同一直线上时,
即点E在对角线AC上时,EA最短,
此时CF旋转了135°,
由勾股定理可得:CF=![]()
则CF扫过的面积为![]() .
.
【解析】(1)根据正方形的性质和全等三角形的判定方法可证明△BCG≌△DCE,由全等三角形的性质即可得到BG=DE;
(2)根据C、E、A三点在同一直线上时,EA最短,再根据勾股定理解答即可.
【考点精析】利用正方形的性质对题目进行判断即可得到答案,需要熟知正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.

练习册系列答案
相关题目