题目内容
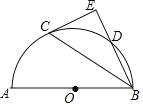
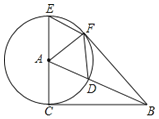
【题目】如图,在![]() △ABC中,∠ACB=
△ABC中,∠ACB=![]() ,以点A为圆心,AC为半径,作⊙A,交AB于点D,交CA的延长线于点E,过点E作AB的平行线EF,交⊙A于点F,连接AF,BF,DF.
,以点A为圆心,AC为半径,作⊙A,交AB于点D,交CA的延长线于点E,过点E作AB的平行线EF,交⊙A于点F,连接AF,BF,DF.
(1)求证:BF是⊙A的切线;
(2)当∠CAB等于多少度时,四边形ADFE为菱形?请给与证明.
(3)若EF=1,AE=2,求cos∠CBA的值.
【答案】(1)见解析;(2)∠CAB=![]() ,四边形ADFE为菱形,理由见解析.(3)
,四边形ADFE为菱形,理由见解析.(3)![]()
【解析】
(1)根据平行线的性质得∠E=∠CAB,∠EFA=∠FAB,加上∠E=∠EFA,则∠FAB=∠CAB,于是可判断△ABC≌△ABF,从而得到∠AFB=90°,然后根据切线的判定方法可判断BF是⊙A的切线;
(2)当∠CAB=60°,则∠FAB=∠EAF=60°,于是可证△AEF和△ADF都为等边三角形,所以AE=EF=AD=DF,然后根据菱形的判定方法可判断此时四边形ADFE是菱形;
(3)连接FC,证明∠ACF=∠CBA即可.
(1)证明:∵EF∥AB,
∴∠E=∠CAB,∠EFA=∠FAB,
∵∠E=∠EFA,
∴∠FAB=∠CAB,
在△ABC和△ABF中,
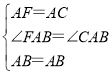 ,
,
∴△ABC≌△ABF(SAS),
∴∠AFB=∠ACB=90°,
∴BF⊥AF,
∵AF是⊙A的半径,
∴BF是⊙A的切线;
(2)解:当∠CAB=60°时,四边形ADFE为菱形.
理由如下:∵∠CAB=60°,
∴∠FAB=∠EAF=60°,
∵AE=AF=AD,
∴△AEF和△ADF都为等边三角形,
∴AE=EF=AD=DF,
∴四边形ADFE是菱形.
(3)连FC,

∵EC为直径,
∴∠EFC=90°
∵EF=1,AE=2,
∴FC=![]() ,
,
∵A为EC的中点,EF∥AB,
∴AB垂直平分线FC,交AB于P,则CP= ![]()
又∠ABC=∠ACP
cos∠ABC=![]() ∠ACP=
∠ACP=![]() =
=![]()

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】为监控某条生产线上产品的质量,检测员每个相同时间抽取一件产品,并测量其尺寸,在一天的抽检结束后,检测员将测得的个数据按从小到大的顺序整理成如下表格:
编号 | ① | ② | ③ | ④ | ⑤ | ⑥ | ⑦ | ⑧ | ⑨ | ⑩ | |||||
尺寸(cm) | 8.72 | 8.88 | 8.92 | 8.93 | 8.94 | 8.96 | 8.97 | 8.98 | a | 9.03 | 9.04 | 9.06 | 9.07 | 9.08 | b |
按照生产标准,产品等次规定如下:
尺寸(单位:cm) | 产品等次 |
8.97≤x≤9.03 | 特等品 |
8.95≤x≤9.05 | 优等品 |
8.90≤x≤9.10 | 合格品 |
x<8.90或x>9.10 | 非合格品 |
注:在统计优等品个数时,将特等品计算在内;在统计合格品个数时,将优等品(含特等品)仅算在内.
(1)已知此次抽检的合格率为80%,请判断编号为的产品是否为合格品,并说明理由
(2)已知此次抽检出的优等品尺寸的中位数为9cm.
(i)求a的值,
(ii)将这些优等品分成两组,一组尺寸大于9cm,另一组尺寸不大于9cm,从这两组中各随机抽取1件进行复检,求抽到的2件产品都是特等品的概率.