��Ŀ����
����Ŀ��Ϊ���˽�ѧ����ע�ȵ����ŵ�����������ᡱ�ڼ䣬С���༶ͬѧһ�����տ������ᡱ���ŵĴ���������˵��飬������ͳ����ͼ��ʾ�����������տ�3�ε�����û�б����������������Ϣ��������и��⣺
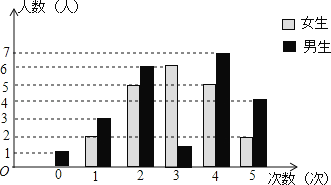
��1���ð༶Ů�������� ��Ů���տ������ᡱ���Ŵ����������� ����λ���� ��
��2����Ů���տ�������ƽ������
��3��Ϊ��һ�������ð༶�С�Ů���տ������ᡱ���Ŵ������ص㣬С�������Ů���տ������ᡱ���Ŵ����ķ���Ϊ![]() �������տ������ᡱ���Ŵ����ķ���Ϊ2����Ƚϸð༶�С�Ů���տ������ᡱ���Ŵ����IJ�����С��
�������տ������ᡱ���Ŵ����ķ���Ϊ2����Ƚϸð༶�С�Ů���տ������ᡱ���Ŵ����IJ�����С��
��4������ij��Ⱥ�壬���ǰ�һ�����տ�ij�ȵ����Ŵ���������3�ε�����ռ������Ⱥ���������İٷֱȽ�����Ⱥ���ij�ȵ����ŵġ���עָ����������ð༶�����ԡ����ᡱ���ŵġ���עָ������Ů����5%������ð༶����������
���𰸡���1��20���ˣ�������Ϊ3����λ����3����2��30����3��������Ů���IJ������ȴ���4��������25�ˣ�
��������
�����������1�������ۿ�������������ӵõ�Ů���������ۿ���������Ϊ��������С�������к����м���м�������ƽ��Ϊ��λ����
��2�����ݼ�Ȩƽ�������㷨����ʽ���㼴�ɣ�
��3���ɷ�����жϣ�����С˵������С��
��4���������⣬���Ů���Ĺ�עָ���������õ������Ĺ�עָ��������������Ϊx���г����̣���֮�ɵã�
�⣺��1���ð༶Ů������Ϊ��2+5+6+5+2=20���ˣ���
�����տ�3�ε�������࣬��6�Σ�������Ϊ3��
�ð༶Ů���տ���������λ���Ǵ�С�������еĵ�10��11������ƽ��������Ϊ3������λ����3��
��2��Ů���տ�������ƽ�����ǣ�![]() ����1��2+2��5+3��6+4��5+5��2��=
����1��2+2��5+3��6+4��5+5��2��=![]() =30��
=30��
��3����2��![]() ��
��
������������Ů���IJ������ȴ�
��4�������⣺�ð�Ů���ԡ����ᡱ���ŵġ���עָ����Ϊ![]() ��100%=65%��
��100%=65%��
���ԣ������ԡ����ᡱ���ŵġ���עָ����Ϊ60%
��������x��
��![]() ��
��
��ã�x=25��
�𣺸ð༶������25�ˣ�

����Ŀ��������y=��x2+bx+c�ϲ��ֵ�ĺ�����x��������y�Ķ�Ӧֵ���±���
x | �� | ��2 | ��1 | 0 | 1 | 2 | �� |
y | �� | 0 | 4 | 6 | 6 | 4 | �� |
���ϱ���֪������˵����ȷ�ĸ����ǣ� ��
����������x���һ������Ϊ����2��0��������������y��Ľ���Ϊ��0��6�����������ߵĶԳ�����x=1�����ڶԳ������y��x���������
A��1 B��2 C��3 D��4