题目内容
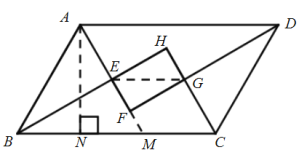
【题目】如图在平行四边形ABCD中,∠ABC=60°,AB=4,四条内角平分线围成四边形EFGH面积为![]() ,则平行四边形ABCD面积为________
,则平行四边形ABCD面积为________

【答案】![]()
【解析】
先证明四边形EFGH为矩形,再利用矩形的面积计算出EG的长,从而进一步计算平行四边形ABCD的面积.
延长AF交BC于点M,过点A作AN⊥BC于点N,连接EG
∵四边形ABCD是平行四边形
∴AD∥BC
又∵∠ABC=60°
∴∠BAD=180°-60°=120°
又∵BH、AF分别平分∠ABC、∠BAD
∴∠ABH=![]() ,∠BAE=
,∠BAE=![]()
∴∠HEF=∠AEB=![]()
同理,∠H=∠HGF=90°
在四边形EFGH中,∠H=∠HEF=∠HGF=90°
∴四边形EFGH为矩形
在△ABM中,∠ABM=∠BAM=60°
∴△ABM为等边三角形
又∵BE平分∠ABM,AB=4
∴![]()
同理可得,![]()
∴![]()
∵四边形EFGH为矩形
∴EM∥CG
∵![]() 且EM∥CG
且EM∥CG
∴四边形EMCG为平行四边形
∴EG∥CM
∴∠HEG=∠HBC=30°
∴![]()
不妨设HG=a,EG=2a,
则由勾股定理可得![]()
∵四边形EFGH面积为![]()
∴![]()
∴![]()
∴CM=EG=2a=2
在Rt△ABN中,∠ABN=60°, ∠ANB=90°,AB=4
∴![]() ,
,![]()
∴![]()
故答案为:![]() .
.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目