题目内容
【题目】如图,∠MON=90°,正方形ABCD的顶点A、B分别在OM、ON上,AB=13,OB=5,E为AC上一点,且∠EBC=∠CBN,直线DE与ON交于点F.
(1)求证BE=DE;
(2)判断DF与ON的位置关系,并说明理由;
(3)△BEF的周长为 .

【答案】(1)见解析;(2)DF⊥ON,理由见解析;(3)24
【解析】
(1)根据正方形的性质证明△BCE≌△DCE即可;
(2)由第一题所得条件和已知条件可推出∠EDC=∠CBN,再利用90°的代换即可证明;
(3)过D点作DG垂直于OM,交点为G,结合已知条件推出DF和BF的长,再根据第一题结论得出△BEF的周长等于DF加BF即可得出答案.
解:(1)证明:∵四边形ABCD正方形,
∴CA平分∠BCD,BC=DC,
∴∠BCE=∠DCE=45°,
∵CE=CE,
∴△BCE≌△DCE(SAS);
∴BE=DE;
(2)DF⊥ON,理由如下:
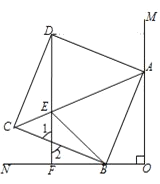
∵△BCE≌△DCE,
∴∠EBC=∠EDC,
∵∠EBC=∠CBN,
∴∠EDC=∠CBN,
∵∠EDC+∠1=90°,∠1=∠2,
∴∠2+∠CBN=90°,
∴∠EFB=90°,即DF⊥ON;
(3)过D点作DG垂直于OM,交点为G,
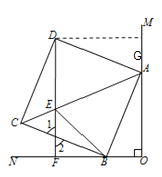
∵四边形ABCD是正方形,
∴AD=AB,∠BAD=90°,
∴∠DAG+∠BAO=90°,
∵∠ABO+∠BAO=90°,
∴∠DAG=∠ABO,
又∵∠MON=90°,DG⊥OM,
∴△ADG≌△ABO,
∴DM=AO,GA=OB=5,
∵AB=13,OB=5,
根据勾股定理可得AO=12,
由(2)可知DF⊥ON,
又∵∠MON=90°,DG⊥OM,
∴四边形OFDM是矩形,
∴OF=DG=AO=12,DF=OM=17,
由(1)可知BE=DE,
∴△BEF的周长=DF+BF=17+(12-5)=24.





