题目内容
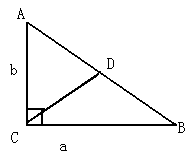
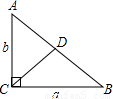
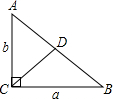已知：在RT△ACB中，∠ACB=90°，CD是斜边上的中线，CD=4，且a+b=10，请你利用所学知识求△ACB的面积．
解：∵CD是斜边AB上的中线，CD=4，
∴AB=8（直角三角形中斜边上的中线是斜边的一半）；
∵a+b=10①，∠ACB=90°，
∴a2+b2=82②；
将①式两边平方得，a2+2ab+b2=100③；
③-②得，2ab=100-64，
∴ab=18；
∴S△ACB=
ab=9．
（其他方法也可以，比如用一元二次方程解出，然后算出面积）
分析：根据已知可求得AB的长，再利用勾股定理及完全平方公式即可求得ab的值，从而根据三角形的面积公式即可求得其面积．
点评：此题主要考查学生对勾股定理及完全平方公式的变形运用能力．
∴AB=8（直角三角形中斜边上的中线是斜边的一半）；
∵a+b=10①，∠ACB=90°，
∴a2+b2=82②；
将①式两边平方得，a2+2ab+b2=100③；
③-②得，2ab=100-64，
∴ab=18；
∴S△ACB=
ab=9．（其他方法也可以，比如用一元二次方程解出，然后算出面积）
分析：根据已知可求得AB的长，再利用勾股定理及完全平方公式即可求得ab的值，从而根据三角形的面积公式即可求得其面积．
点评：此题主要考查学生对勾股定理及完全平方公式的变形运用能力．
练习册系列答案
名校课堂系列答案
相关题目
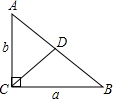已知：在RT△ACB中，∠ACB=90°，CD是斜边上的中线，CD=4，且a+b=10，请你利用所学知识求△ACB的面积．
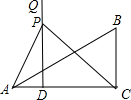重合），过D作DQ⊥AC（DQ与AB在AC的同侧）；点P从D点出发，在射线DQ上运动，连接PA、PC．
