题目内容
【题目】方成同学看到一则材料,甲开汽车,乙骑自行车从M地出发沿一条公路匀速前往N地,设乙行驶的时间为t(h),甲乙两人之间的距离为y(km),y与t的函数关系如图1所示,方成思考后发现了图1的部分正确信息,乙先出发1h,甲出发20分钟后与乙相遇,…,请你帮助方成同学解决以下问题: 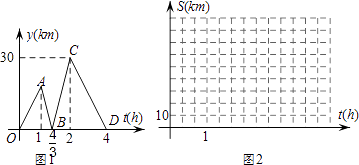
(1)分别求出线段BC,CD所在直线的函数表达式;
(2)当15<y<25时,求t的取值范围;
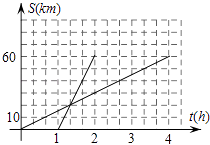
(3)分别求出甲、乙行驶的路程S甲、S乙与时间t的函数表达式,并在图2所给的直角坐标系中分别画出它们的图象.
【答案】
(1)解:设线段BC所在直线的函数表达式为y=k1t+b1,
将点B( ![]() ,0),点C(2,30)代入函数解析式,得
,0),点C(2,30)代入函数解析式,得
 ,解得:
,解得: ![]() .
.
故线段BC所在直线的函数表达式为y=45t﹣60( ![]() ≤t≤2).
≤t≤2).
设线段CD所在直线的函数表达式为y=k2t+b2,
将点C(2,30),点D(4,0)代入函数解析式,得
![]() ,解得:
,解得: ![]() .
.
故线段CD所在直线的函数表达式为y=﹣15t+60(2<t≤4)
(2)解:乙骑车的速度为30÷(4﹣2)=15(km/h),
∴线段OA所在直线的函数表达式为y=15t(0≤t≤1),
∴点A的纵坐标为15.
当15<y<25时,即15<45t﹣60<25或15<﹣15t+60<25,
解得: ![]() <t<
<t< ![]() 或
或 ![]() <t<3.
<t<3.
故当15<y<25时,t的取值范围为 ![]() <t<
<t< ![]() 或
或 ![]() <t<3
<t<3
(3)解:甲开车的速度15÷( ![]() ﹣1)+15=60(km/h),
﹣1)+15=60(km/h),
∴S甲=60(t﹣1)=60t﹣60(1≤t≤2),S乙=15t(0≤t≤4).
所画图形如图.
【解析】(1)设线段BC所在直线的函数表达式为y=k1t+b1 , 将点B、C的坐标代入其中得出关于k1、b1的二元一次方程组,解方程组即可求出结论;设线段CD所在直线的函数表达式为y=k2t+b2 , 将点C、D的坐标代入其中得出关于k2、b2的二元一次方程组,解方程组即可得出结论;(2)根据线段CD可求出乙骑车的速度,从而得出线段OA的函数解析式,结合题意列出关于t的一元一次不等式,解不等式即可得出结论;(3)根据图象求出甲开车的速度,由路程=速度×时间得出S甲、S乙与时间t的函数表达式,画出图形即可.

 一线名师提优试卷系列答案
一线名师提优试卷系列答案



