题目内容
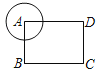
【题目】如图,在矩形ABCD中,AB=6,AD=8,以顶点A为圆心作半径为r的圆,若要求另外三个顶点至少有一个在圆内,且至少有一个在圆外,则r的取值范围是_____.
【答案】6<r<10.
【解析】
要确定点与圆的位置关系,主要根据点与圆心的距离与半径的大小关系来进行判断.即当d>r时,点在圆外;当d=r时,点在圆上;当d<r时,点在圆内.再根据三个顶点至少有一个在圆内,且至少有一个在圆外分析计算即可.
解:∵四边形ABCD为矩形,
∴CD=AB=6,又AD=8,
∴AC=![]() =10.
=10.
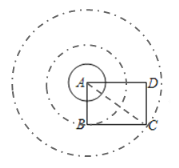
由图可知,
当圆经过点B时,r=6,点B在圆上,C,D两点在圆外,∴r>6;
当圆经过点C时,r=10,点C在圆上,B,D都在圆内,∴r<10,
∴6<r<10.
故答案为:6<r<10.

练习册系列答案
相关题目