题目内容
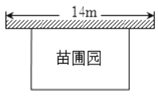
【题目】如图所示,为了改造小区环境,某小区决定要在一块一边靠墙(墙的最大可使用长度12m)的空地上建造一个矩形绿化带.除靠墙一边(AD)外,用长为32m的栅栏围成矩形ABCD.设绿化带宽AB为xm,面积为Sm2,
(1)求S与x的函数关系式,并直接写出x的取值范围;
(2)绿化带的面积能达到128m2吗?若能,请求出AB的长度;若不能,请说明理由;
(3)当x为何值时,满足条件的绿化带面积最大.

【答案】(1)S=﹣2x2+32x(10≤x<16);(2)绿化带的面积不能达到128m2,理由详见解析;(3)当x=10时,绿化带面积最大.
【解析】
(1)依题意易可得BC=32-2x,根据矩形的面积公式可得出S与x的函数关系式,再由0<32-2x≤12可求出x的取值范围;
(2)先将S=128代入(1)中的解析式,求出x,再根据x的取值范围判断即可;
(3)将(1)中的函数关系式化为顶点式,再结合x的取值范围利用二次函数的性质可求得结果.
解:(1)由题意得,BC=32-2x,
∴S=x(32﹣2x)=﹣2x2+32x,
又0<32-2x≤12,解得10≤x<16,
故S与x的函数关系式为S=﹣2x2+32x(10≤x<16);
(2)根据题意得,当S=128时,有﹣2x2+32x=128,
解得:x=8,
又由(1)知10≤x<16,
∴x=8不符合题意,
故绿化带的面积不能达到128m2;
(3)∵S=﹣2x2+32x=﹣2(x﹣8)2+128,
当10≤x<16,y随x的增大而减小,
∴当x=10时,绿化带面积最大.

练习册系列答案
相关题目