题目内容
已知:抛物线y=-x2+mx+2m2(m>0)与x轴交于A、B两点,点A在点B的左边,C是抛物线上一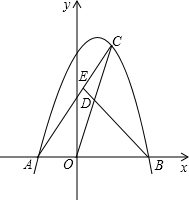 个动点(点C与点A、B不重合),D是OC的中点,连接BD并延长,交AC于点E.
个动点(点C与点A、B不重合),D是OC的中点,连接BD并延长,交AC于点E.(1)用含m的代数式表示点A、B的坐标;
(2)求
| CE |
| AE |
(3)当C、A两点到y轴的距离相等,且S△CED=
| 8 |
| 5 |
分析:(1)由y=0,得出的一元二次方程的解就是A、B两点的横坐标.由此可求出A、B的坐标.
(2)本题要通过构建相似三角形求解,过O作OG∥AC交BE于G,那么可得出两组相似三角形:△CED∽△OGD、△BOG∽△BAE,可分别用这两组相似三角形得出OG与EC的比例关系、OG与AE的比例关系,从而得出CE、AE的比例关系.
(3)求直线BE的解析式,要知道B、D的坐标,就要先确定m的值,已知了A、C到y轴的距离相等,因此A、C的横坐标互为相反数,可得出C的坐标为(m,2m2).连接OE,可根据(2)中AE、CE的比例关系得出△CED与△AOC的面积比,从而可求出△AOC的面积,根据A、C两点的坐标即可表示出三角形AOC的面积,由此可确定m的值.即可得出A、C、B的坐标.也就能求出D点的坐标,然后根据B、D的坐标用待定系数法求出直线BE的解析式.
(2)本题要通过构建相似三角形求解,过O作OG∥AC交BE于G,那么可得出两组相似三角形:△CED∽△OGD、△BOG∽△BAE,可分别用这两组相似三角形得出OG与EC的比例关系、OG与AE的比例关系,从而得出CE、AE的比例关系.
(3)求直线BE的解析式,要知道B、D的坐标,就要先确定m的值,已知了A、C到y轴的距离相等,因此A、C的横坐标互为相反数,可得出C的坐标为(m,2m2).连接OE,可根据(2)中AE、CE的比例关系得出△CED与△AOC的面积比,从而可求出△AOC的面积,根据A、C两点的坐标即可表示出三角形AOC的面积,由此可确定m的值.即可得出A、C、B的坐标.也就能求出D点的坐标,然后根据B、D的坐标用待定系数法求出直线BE的解析式.
解答:解:(1)∵抛物线y=-x2+mx+2m2(m>0)与x轴交于A、B两点,
∴关于x的方程-x2+mx+2m2=0有两个不相等的实数根x1和x2;
解得x1=-m,x2=2m.
∵点A在点B的左边,且m>0,
∴A(-m,0),b(2m,0).
(2)过点O作OG∥AC交BE于点G.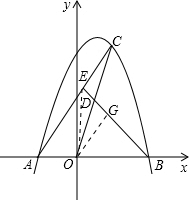
∴△CED∽△OGD
∴
=
;
∵DC=DO,
∴CE=OG;
∵OG∥AC,
∴△BOG∽△BAE,
∴
=
.
∵OB=2m,AB=3m.
∴
=
=
=
.
(3)连接OE.
∵D是OC的中点,
∴S△OCE=2S△CED
∵
=
=
∴
=
.
∴S△AOC=5S△CED=8
∵S△AOC=
OA•|yC|=
m•2m2=m3
∴m3=8,
解得m=2.
∴抛物线的解析式为y=-x2+2x+8,点C的坐标为(2,8),点B的坐标为(4,0).
分别过点D、C作x轴的垂线,交x轴于点M、N.
∴DM∥CN,
∵D是OC的中点.
∴OM=
ON=1,DM=
CN=4,
∴点D的坐标为(1,4).
设直线BE的解析式为y=kx+b,则有:
,
解得:
,
∴直线BE的解析式为y=-
x+
.
∴关于x的方程-x2+mx+2m2=0有两个不相等的实数根x1和x2;
解得x1=-m,x2=2m.
∵点A在点B的左边,且m>0,
∴A(-m,0),b(2m,0).
(2)过点O作OG∥AC交BE于点G.

∴△CED∽△OGD
∴
| DC |
| DO |
| CE |
| OG |
∵DC=DO,
∴CE=OG;
∵OG∥AC,
∴△BOG∽△BAE,
∴
| OG |
| AE |
| OB |
| AB |
∵OB=2m,AB=3m.
∴
| CE |
| AE |
| OG |
| AE |
| OB |
| AB |
| 2 |
| 3 |
(3)连接OE.
∵D是OC的中点,
∴S△OCE=2S△CED
∵
| S△OCE |
| S△AOC |
| CE |
| CA |
| 2 |
| 5 |
∴
| S△CED |
| S△AOC |
| 1 |
| 5 |
∴S△AOC=5S△CED=8
∵S△AOC=
| 1 |
| 2 |
| 1 |
| 2 |
∴m3=8,
解得m=2.
∴抛物线的解析式为y=-x2+2x+8,点C的坐标为(2,8),点B的坐标为(4,0).
分别过点D、C作x轴的垂线,交x轴于点M、N.
∴DM∥CN,
∵D是OC的中点.
∴OM=
| 1 |
| 2 |
| 1 |
| 2 |
∴点D的坐标为(1,4).
设直线BE的解析式为y=kx+b,则有:
|
解得:
|
∴直线BE的解析式为y=-
| 4 |
| 3 |
| 16 |
| 3 |
点评:本题着重考查了相似三角形和二次函数的综合应用等知识点,综合性较强,考查学生数形结合的数学思想方法.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知:抛物线y=x2-6x+c的最小值为1,那么c的值是( )
| A、10 | B、9 | C、8 | D、7 |