题目内容
在反比例函数y=| k | x |
分析:因为方程x2-nx+n-1=0有两个相等的实数根,可得△=0,进而可求出n的值;再根据△ABC的面积等于6,求出A的纵坐标即可.
解答:解:因为方程x2-nx+n-1=0有两个相等的实数根,
所以△=0,
即n2-4(n-1)=0,
解得n1=n2=2.
设三角形的高为h,
又因为AC=4-1=3,三角形面积等于6,
所以
×3h=6,
解得h=4.
由于A可在x轴的上方,也可在x轴的下方,
所以A的纵坐标为±4.
则A点坐标为(2,4)或(2,-4).
分别代入y=
,得:
①k=2×4=8;
②k=2×(-4)=-8.
于是反比例函数解析式为y=
或y=-
.
所以△=0,
即n2-4(n-1)=0,
解得n1=n2=2.
设三角形的高为h,
又因为AC=4-1=3,三角形面积等于6,
所以
| 1 |
| 2 |
解得h=4.
由于A可在x轴的上方,也可在x轴的下方,
所以A的纵坐标为±4.
则A点坐标为(2,4)或(2,-4).
分别代入y=
| k |
| x |
①k=2×4=8;
②k=2×(-4)=-8.
于是反比例函数解析式为y=
| 8 |
| x |
| 8 |
| x |
点评:本题不仅考查了一元二次方程根与系数的关系,还考查了根据面积求三角形的高的能力,解答时要注意分类讨论.

练习册系列答案
相关题目
已知点(3,6)在反比例函数y=
(k≠0)的图象上,那么下列各点中在此函数图象上的点是( )
| k |
| x |
| A、(-3,6) |
| B、(3,-6) |
| C、(2,-9) |
| D、(2,9) |
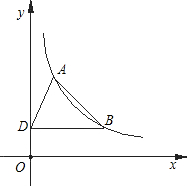 点B作y轴的垂线,垂足为D,连接AD.
点B作y轴的垂线,垂足为D,连接AD. (2013•西宁)如图,正方形AOCB在平面直角坐标系xoy中,点O为原点,点B在反比例函数
(2013•西宁)如图,正方形AOCB在平面直角坐标系xoy中,点O为原点,点B在反比例函数 (2013•泉州质检)如图,在方格纸中(小正方形的边长为1),直线AB与两坐标轴交于格点A、B,根据所给的直角坐标系(O是坐标原点),解答下列问题:
(2013•泉州质检)如图,在方格纸中(小正方形的边长为1),直线AB与两坐标轴交于格点A、B,根据所给的直角坐标系(O是坐标原点),解答下列问题: