题目内容
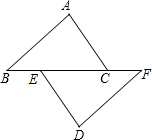 已知:点B、E、C、F在同一条直线上,AB=DF,∠A=∠D,AC∥DE.
已知:点B、E、C、F在同一条直线上,AB=DF,∠A=∠D,AC∥DE.求证:(1)△ABC≌△DEF;
(2)AB∥FD;
(3)BE=CF.
分析:(1)根据平行线性质得出∠DEF=∠ACB,根据AAS推出△ABC≌△DEF即可.
(2)根据全等三角形性质得出∠B=∠F,根据平行线的判定推出即可.
(3)根据全等三角形性质得出BC=EF,即可求出答案.
(2)根据全等三角形性质得出∠B=∠F,根据平行线的判定推出即可.
(3)根据全等三角形性质得出BC=EF,即可求出答案.
解答:证明:(1)∵AC∥DE,
∴∠DEF=∠ACB,
在△ABC和△DEF中
∴△ABC≌△DEF(AAS);
(2)∵△ABC≌△DEF,
∴∠B=∠F,
∴AB∥FD;
(3)∵△ABC≌△DEF,
∴BC=EF,
∴BC-EC=EF-EC,
∴BE=CF.
∴∠DEF=∠ACB,
在△ABC和△DEF中
|
∴△ABC≌△DEF(AAS);
(2)∵△ABC≌△DEF,
∴∠B=∠F,
∴AB∥FD;
(3)∵△ABC≌△DEF,
∴BC=EF,
∴BC-EC=EF-EC,
∴BE=CF.
点评:本题考查了平行线的判定,全等三角形的性质和判定的应用,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS.全等三角形的对应边相等,对应角相等.

练习册系列答案
相关题目
 如图,已知动点P在函数y=
如图,已知动点P在函数y= 如图,已知C点为线段AB的中点,D点为BC的中点,AB=10cm,求AD的长度.
如图,已知C点为线段AB的中点,D点为BC的中点,AB=10cm,求AD的长度. 如图,已知A点的坐标为(2,0),点B在直线y=-x上运动,当线段AB最短时,点B的坐标为( )
如图,已知A点的坐标为(2,0),点B在直线y=-x上运动,当线段AB最短时,点B的坐标为( ) 一个有弹性的球从A点落下到地面,弹起后,到B点又落到高为20cm的平台上,再弹起到C点,然后,又落到地面(如图),每次弹起的高度为落下高度的
一个有弹性的球从A点落下到地面,弹起后,到B点又落到高为20cm的平台上,再弹起到C点,然后,又落到地面(如图),每次弹起的高度为落下高度的