Question

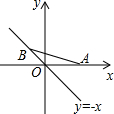如图，已知A点的坐标为（2，0），点B在直线y=-x上运动，当线段AB最短时，点B的坐标为（　　）

• A．（0，0）
• B．（

  2

  ，-

  2

  ）
• C．（1，-1）
• D．（-

  2

  ，

  2

  ）

Answer 1

分析：当AB与直线y=-x垂直时，AB最短，则△OAB是等腰直角三角形，作BD⊥x轴即可求得OD，BD的长，从而求得B的坐标．

解答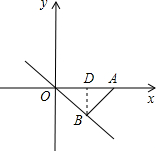：解：当AB与直线y=-x垂直时，AB最短．
∵直线y=-x是第二、四象限的角平分线，
∴△OAB是等腰直角三角形．
作BD⊥x轴，
∴DO=BD=

1

2

OA=1，
∴B的坐标是（1，-1）．
故选C．

点评：本题考查了一次函数与等腰三角形的性质的综合应用，正确根据垂线段最短确定：当AB与直线y=-x垂直时，AB最短是关键．