题目内容
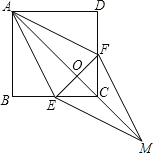
【题目】如图1，用形状相同、大小不等的三块直角三角形木板，恰好能拼成如图2所示的四边形ABCD，若AE=4，CE=3BE，那么这个四边形的面积是 ．
【答案】16
【解析】
试题分析：依题意可以得到△ABE∽△ECD∽△DEA，∠B=∠C=∠D=90°，利用相似三角形的性质可以推出BE：CD=AB：EC，而四边形ABCD为矩形，可以得到AB=CD，所以AB2=BEEC，又因为CE=3BE，可以得到AB=
BE，由此可以求出BE，CB，最后就可以求出面积．
∵形状相同、大小不等的三块直角三角形木板， ∴△ABE∽△ECD∽△DEA，∠B=∠C=∠AED=90°，
∴BE：CD=AB：EC， ∴四边形ABCD为矩形， ∴AB=CD， ∴
=BEEC，
∵CE=3BE， ∴AB=BE， ∵AE=4， ∴BE=2，AB=2， ∴BC=BE+CE=4BE=8，
∴这个四边形的面积是S=AB×BC=2×8=16．
练习册系列答案
相关题目
