题目内容
某超市在销售中发现:某种新年吉祥物品平均每天可售出20套,每套盈利40元。为了迎接新年,商场决定采取适当的降价措施,扩大销售量,增加盈利,尽快减少库存。经市场调查发现:如果每套降价1元,那么平均每天就可多售出2套。要想平均每天在销售这种吉祥物上盈利1200元,那么每套应降价多少?
20元.
试题分析:设每套降价x元,那么就多卖出2x套,根据扩大销售量,增加盈利,尽快减少库存,每天在销售吉祥物上盈利1200元,可列方程求解.
试题解析:设每套降价x元,
由题意得:(40-x)(20+2x)=1200
即2x2-60x+400=0,
∴x2-30x+200=0,
∴(x-10)(x-20)=0,
解之得:x=10或x=20
为了减少库存,所以x=20.
因此,每套应降价20元.
考点: 一元二次方程的应用.

练习册系列答案
相关题目
 满足条件
满足条件 时,求出方程
时,求出方程 的根
的根
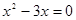 的根是 .
的根是 . 的根是( )
的根是( )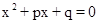 的根的判别式是_________________.
的根的判别式是_________________.