题目内容
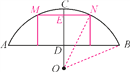
【题目】如图,某地有一座圆弧形拱桥,桥下水面宽度AB为7.2 m,拱高CD为2.4 m.
(1)求拱桥的半径;
(2)现有一艘宽3 m,船舱顶部为长方形并高出水面2 m的货船要经过这里,问此货船能顺利通过拱桥吗?

【答案】(1)拱桥的半径为3.9 m;(2)此货船能顺利通过拱桥.
【解析】 试题分析:(1)连接OB,根据垂径定理求出BD,设OB=OC=r,再在Rt△BOD中利用勾股定理求出r;(2)作出拱桥下的矩形,交拱桥于M,N,交CD于E,连接ON,通过求距离水面2米高处即ED长为2时,桥有多宽,即MN的长,当货船顶部宽度大于MN则货船不能通过,当货船顶部宽度小于等于MN则货船能通过.
解:(1)连接OB.
∵OC⊥AB,∴D为AB的中点.
∴BD=![]() AB=3.6(m).
AB=3.6(m).
设OB=OC=r,则OD=(r-2.4)m.
在Rt△BOD中,OB2=OD2+BD2,即r2=(r-2.4)2+3.62,解得r=3.9.
∴拱桥的半径为3.9 m.
(2)作出拱桥下的矩形,交拱桥于M,N,交CD于E,连接ON.
∵CD=2.4 m,DE=2 m,
∴CE=CD-DE=0.4(m).
∴OE=OC-CE=3.9-0.4=3.5(m).
在Rt△OEN中,EN=![]() =
=![]() =
=![]() (m2),
(m2),
∵OD⊥MN,
∴MN=2EN=2×![]() ≈3.44 m>3 m.
≈3.44 m>3 m.
∴此货船能顺利通过拱桥.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案
相关题目


