题目内容
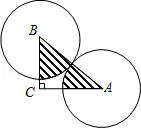
如图,在破残的圆形残片上,弦AB的垂直平分线交弧AB于点C,交弦AB于点D,已知AB=8cm,CD=2cm.

(1)求作此残片所在的圆(不写作法,保留作图痕迹);
(2)求出(1)中所作圆的半径.

(1)求作此残片所在的圆(不写作法,保留作图痕迹);
(2)求出(1)中所作圆的半径.
详见解析
试题分析:(1)求此残片所在的圆,关键是找出该圆的圆心,而两条直径的交点即为圆心。由垂径定理可知直线CD经过圆心,因此可在该圆上另外任意画一段弧,作出其垂直平分线,则两条直线的交点即为所求圆的圆心.
(2)如图,由垂径定理可得
 ,设圆P的半径为
,设圆P的半径为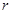 ,则
,则 ,利用勾股定理即可求解.
,利用勾股定理即可求解.试题解析:
解:(1)如下图:以P为圆心,AP为半径的圆即为此残片所在的圆.

(2)设圆P的半径为
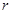 ,
,∵
 ,
, ,
,
∴
 ,
,
在
 中,
中,
∴

解得

∴⊙P的半径为5cm.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目




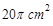





 中,
中, ,AC=8,BC=6,两等圆
,AC=8,BC=6,两等圆 、
、 外切,那么图中两个扇形(即阴影部分)的面积之和为 。
外切,那么图中两个扇形(即阴影部分)的面积之和为 。