题目内容
【题目】阅读下面材料:
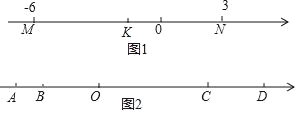
如图1,在数轴上点M表示的数是﹣6,点N表示的数是3,求线段MN的中点K所示的数.
对于求中点表示数的问题,只要用点N所表示的数3,加上点M所表示的数﹣6,得到的结果再除以2,就可以得到中点K所表示的数;即K点表示的数为![]() =﹣1.5
=﹣1.5
利用材料中知识解决下面问题:
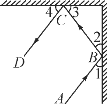
如图2,已知数轴上有A、B、C、D四点,A点表示数为﹣6,B点表示的数是﹣4,线段AD=18,BC=3CD.
(1)点D所表示的数是 ;
(2)若点B以每秒4个单位的速度向右运动,点D以每秒1个单位的速度向左运动,同时运动t秒后,当点C为线段BD的中点时,求t的值;
(3)若(2)中点B、点D的运动速度运动方向不变,点A以每秒10个单位的速度向右运动,点C以每秒3个单位的速度向左运动,点P是线段AC的中点,点Q是线段BD的中点,A、B、C、D四点同时运动,运动时间为t,求线段PQ的长(用含t的式子表示).
【答案】(1)12;(2)![]() ;(3)线段PQ的长为2t﹣3或3﹣2t.
;(3)线段PQ的长为2t﹣3或3﹣2t.
【解析】
(1)由两点间的距离可求出AD、OA、 OD的长,在根据他们之间的关系可得D点表示的数;
(2)可求出AB、 BD、 BC 、CD、 OC即C点的坐标,由点C为线段BD的中点时,可求得t;
(2)分P点再Q点左侧和右侧两种情况讨论即可.
(1)∵AD=18,OA=6,
∴OD=18﹣6=12,
∴D点表示的数是12;
故答案为:12;
(2)∵A点表示数为﹣6,B点表示的数是﹣4,
∴AB=2,
∴BD=16,
∵BC=3CD,
∴BC=12,CD=4,
∴OC=12﹣4=8,
∴C(8,0),
由题意得:B(﹣4+4t,0),D(12﹣t,0),
∴![]() =8,
=8,
t=![]() ;
;
(3)运动后:A:﹣6+10t,
C:8﹣3t,
∴P:![]() =
=![]() ,
,
B:﹣4+4t,
D:12﹣t,
∴Q:![]() =
=![]() ,
,
当![]() ≥
≥![]() 时,t
时,t![]() ,PQ=
,PQ=![]() =2t﹣3,
=2t﹣3,
当![]() <
<![]() 时,t<
时,t<![]() ,PQ=
,PQ=![]() ﹣
﹣![]() =3﹣2t.
=3﹣2t.
综上,线段PQ的长为2t﹣3或3﹣2t.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某商场为了迎接“6.1儿童节“,以调低价格的方式促销n个不同的玩具,调整后的单价y(元)与调整前的单价x(元)满足一次函数关系,如表:
第1个 | 第2个 | 第3个 | 第4个 | … | 第n个 | |
调整前单价x (元) | x1 | x2=6 | x3=72 | x4 | … | xn |
调整后单价y (元) | y1 | y2=4 | y3=59 | y4 | … | yn |
当这些玩具调整后的单价都大于2元时,解答下列问题:
(1)y与x的函数关系式为,x的取值范围为;
(2)某个玩具调整前单价是108元,顾客购买这个玩具省了元;
(3)这n个玩具调整前、后的平均单价分别为 ![]() (元)、
(元)、 ![]() (元),猜想
(元),猜想 ![]() 与
与 ![]() 的关系式,并写出推导过程.
的关系式,并写出推导过程.