��Ŀ����
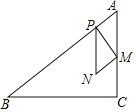
����Ŀ����ͼ���ڡ�ABC�У���C=90�㣬BC��4��AC��3����P��б��AB��һ�㣬����P��PM��AB����AC��BC�ڵ�M���ֹ���P��AC��ƽ���ߣ������M��PM�Ĵ��߽��ڵ�N�����AP��x����PMN���ABC�غϲ���ͼ�ε��ܳ�Ϊy��
��1��AB���� ����
��2������N�ڱ�BC��ʱ��x���� ����
��3����y��x֮��ĺ�����ϵʽ��
��4���ڵ�Nλ��BC�Ϸ��������£�ֱ��д������N���ABCһ�������ֱ��ƽ�֡�ABC���ʱx��ֵ��
���𰸡���1��5����2��![]() ����3�������������4������������x��ֵΪ
����3�������������4������������x��ֵΪ![]() ��
��
��������
��1�����ݹ��ɶ�������ֱ�������2����֤���ı���PAMN��ƽ���ı��Σ��ٸ������Ǻ���ֵ��⣨3�����������t�Ĵ�С�����ͬ�ĺ�����ϵʽ��4����ͬ�����£�����G��AC�е�ʱ�͵���D��AB�е�ʱ���������������ε��������.
�⣺��1����![]() �У�
�У�![]() ,
,
�ʴ�Ϊ5��
��2����ͼ1�У�![]()
���ı���PAMN��ƽ���ı��Σ�
![]()

����![]() ��
��![]() ��ʱ��
��ʱ��![]() ��
��
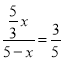
![]() ��
��
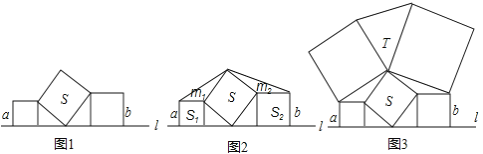
��3���ٵ�![]() ʱ����ͼ1��
ʱ����ͼ1��![]()
![]() ��
��
�ڵ�![]() ʱ����ͼ2��
ʱ����ͼ2��

 y
y
�۵�![]() ʱ����ͼ3��
ʱ����ͼ3��


��4����ͼ4�У�����![]() ��
��![]() �е�ʱ����������
�е�ʱ����������

 .
.
��ͼ5�У�����![]() ��
��![]() �е�ʱ������������
�е�ʱ������������

 .
.
��������������������x��ֵΪ![]() ��
��![]() ��
��

 �����ҵ���������ͯ������ϵ�д�
�����ҵ���������ͯ������ϵ�д�����Ŀ��ijУ��֯���꼶ѧ���μӺ�����д�������������ȡ����ѧ���ɼ���Ϊ�������з��������Ƴ����µ�ͳ�Ʊ���
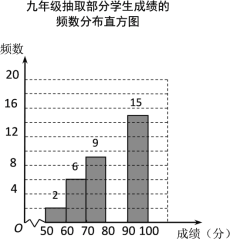
![]()
�ɼ�x/�� | Ƶ�� | Ƶ�� | |
��1�� | x��60 | 2 | 0.04 |
��2�� | 60��x��70 | 6 | 0.12 |
��3�� | 70��x��80 | 9 | b |
��4�� | 80��x��90 | a | 0.36 |
��5�� | 90��x��100 | 15 | 0.30 |
�����������Ϣ������������⣺
��1��a��______��b��______��
��2���벹ȫƵ���ֲ�ֱ��ͼ��
��3�������У�����ѧ���ɼ�����λ�����ڵ�_______����
��4����֪���꼶��400��ѧ���μ���α��������ɼ���90�����ϣ���90�֣���Ϊ�������Ƹ��꼶�ɼ�Ϊ�ŵ��ж����ˣ�