Question

如图，已知点A、B在双曲线y=

k

x

（x＞0）上，AC⊥x轴于C，BD⊥y轴于点D，AC与BD交于点P，P是AC的中点．
（1）试判断四边形ABCD的形状，并说明理由．
（2）若△ABP的面积为3，求该双曲线的解析式．

Answer 1

分析：（1）通过全等三角形Rt△ADP≌Rt△CDP可以判定AD=CD；同理求得AB=BC、AD=AB；所以AB=BC=AD=CD，从而推知四边形ABCD是菱形；
（2）由△ABP的面积为3，知BP•AP=6．根据反比例函数 y=kx中k的几何意义，知本题k=OC•AC，由反比例函数的性质，结合已知条件P是AC的中点，得出OC=BP，AC=2AP，进而求出k的值．

解答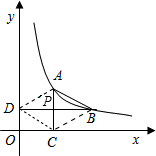：解：（1）菱形．
理由：连接AD、CD、BC；
∵AC⊥x轴于C，BD⊥y轴于点D，
∴AC⊥BD；
设A（m，n），则mn=k，P（m，

1

2

n），
B点纵坐标为

1

2

n，横坐标为

k

1 2 n

=

2mn

n

=2m，
∴PD=PB，
又AP=PC，
∴四边形ABCD是菱形；

（2）∵△ABP的面积为

1

2

•BP•AP=3，
∴BP•AP=6，
∵P是AC的中点，
∴A点的纵坐标是B点纵坐标的2倍，
又∵点A、B都在双曲线y=

k

x

（x＞0）上，
∴B点的横坐标是A点横坐标的2倍，
∴OC=DP=BP，
∴k=OC•AC=BP•2AP=12．
∴该双曲线的解析式是：y=

12

x

．

点评：主要考查了反比例函数 y=

k

x

中k的几何意义，即过双曲线上任意一点引x轴、y轴垂线，所得矩形面积为|k|，是经常考查的一个知识点；这里体现了数形结合的思想，做此类题一定要正确理解k的几何意义．