题目内容
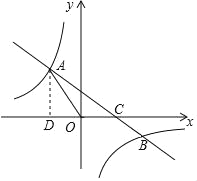
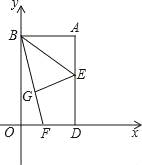
【题目】如图,以矩形ABOD的两边OD、OB为坐标轴建立直角坐标系,若E是AD的中点,将△ABE沿BE折叠后得到△GBE,延长BG交OD于F点.若OF=I,FD=2,则G点的坐标为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】
连结EF,作GH⊥x轴于H,根据矩形的性质得AB=OD=OF+FD=3,再根据折叠的性质得BA=BG=3,EA=EG,∠BGE=∠A=90°,而AE=DE,则GE=DE,于是可根据“HL”证明Rt△DEF≌Rt△GEF,得到FD=FG=2,则BF=BG+GF=5.在Rt△OBF中,利用勾股定理计算出OB,然后根据△FGH∽△FBO,利用相似比计算出GH和FH,根据OH=OF﹣HF,即可得到G点的坐标.
连结EF,作GH⊥x轴于H,如图,
∵四边形ABOD为矩形,
∴AB=OD=OF+FD=1+2=3.
∵△ABE沿BE折叠后得到△GBE,
∴BA=BG=3,EA=EG,∠BGE=∠A=90°.
∵点E为AD的中点,
∴AE=DE,
∴GE=DE.
在Rt△DEF和Rt△GEF中,
∵![]() ,
,
∴Rt△DEF≌Rt△GEF(HL),
∴FD=FG=2,
∴BF=BG+GF=3+2=5.
在Rt△OBF中,OF=1,BF=5,
∴OB![]() .
.
∵GH∥OB,
∴△FGH∽△FBO,
∴![]() ,
,
即![]() ,
,
∴GH![]() ,FH
,FH![]() ,
,
∴OH=OF﹣HF=1![]() ,
,
∴G点坐标为(![]() ).
).
故选B.


练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目