��Ŀ����
����Ŀ����ͼ��ֱ��y=��x+3��x�ύ�ڵ�C����y�ύ�ڵ�B��������y=ax2+ ![]() x+c����B��C���㣬��E��ֱ��BC�Ϸ��������ϵ�һ���㣮
x+c����B��C���㣬��E��ֱ��BC�Ϸ��������ϵ�һ���㣮
��1���������ߵĽ���ʽ��
��2������E��y���ƽ���߽�ֱ��BC�ڵ�M����x���ڵ�F����S��BEC= ![]() ʱ���������E�͵�M�����ꣻ
ʱ���������E�͵�M�����ꣻ
��3���ڣ�2���������£���E��ĺ�����Ϊ1ʱ����EM���Ƿ���ڵ�N��ʹ�á�CMN�͡�CBE���ƣ�������ڣ���ֱ��д����N�����ꣻ��������ڣ���˵�����ɣ�
���𰸡�
��1��
�⣺��ֱ��y=��x+3��x�ύ�ڵ�C����y�ύ�ڵ�B��
���B�������ǣ�0��3������C�������ǣ�3��0����
��y=ax2+ ![]() x+c����B��C���㣬
x+c����B��C���㣬
��  ����ã�
����ã�  ��
��
��y=�� ![]() x2+
x2+ ![]() x+3��
x+3��
��2��
�⣺��ͼ1������E��y���ƽ����EF��ֱ��BC�ڵ�M��EF��x���ڵ�F��
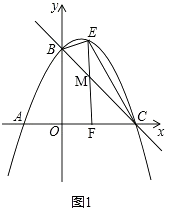
�ߵ�E��ֱ��BC�Ϸ��������ϵ�һ���㣬
�����E�������ǣ�x���� ![]() x2+
x2+ ![]() x+3����
x+3����
���M�������ǣ�x����x+3����
��EM=�� ![]() x2+
x2+ ![]() x+3������x+3��=��
x+3������x+3��=�� ![]() x2+
x2+ ![]() x��
x��
��S��BEC=S��BEM+S��MEC= ![]() EMOC=
EMOC= ![]() ������
������ ![]() x2+
x2+ ![]() x����3=��
x����3=�� ![]() x2+
x2+ ![]() x��
x��
�ੁ ![]() x2+
x2+ ![]() x=
x= ![]() ��
��
��ã�x1=1��x2=2��
����E�������ǣ�1��3����2��2����
��ʱ��Ӧ��M�������ǣ�1��2����2��1����
��3��
�⣺���ڣ�
��B��0��3����E��1��3����
��BE=1����BE��OC��
�ɣ�1��֪OB=OC=3��
���BCO=��CBE=��CMN=45�㣬
��CB=3 ![]() ��CM=2
��CM=2 ![]() ��
��
�ٵ� ![]() =
= ![]() ʱ����CMN�ס�CBE��
ʱ����CMN�ס�CBE��
�� ![]() =
= ![]() ����MN=
����MN= ![]() ��
��
��FN= ![]() ��
��
��N��1�� ![]() ����
����
�ڵ� ![]() =
= ![]() ʱ����CMN�ס�EBC��
ʱ����CMN�ס�EBC��
�� ![]() =
= ![]() ����MN=12��
����MN=12��
��FN=��10��
N�䣨1����10����
����EM�ϴ��ڷ��������ĵ�N��������Ϊ��1�� ![]() ����1����10����
����1����10����

����������1����ֱ��y=��x+3��õ�B��C���꣬���������߽���ʽ���b��c���ɵã���2����E��x���� ![]() x2+
x2+ ![]() x+3������M��x����x+3������֪EM=��
x+3������M��x����x+3������֪EM=�� ![]() x2+
x2+ ![]() x������S��BEC=S��BEM+S��MEC=
x������S��BEC=S��BEM+S��MEC= ![]() EMOC=
EMOC= ![]() �г�����x�ķ��̣���֮�ɵô𰸣���3��������ó���BCO=��CBE=��CMN=45�㡢BE=1��CB=3
�г�����x�ķ��̣���֮�ɵô𰸣���3��������ó���BCO=��CBE=��CMN=45�㡢BE=1��CB=3 ![]() ��CM=2
��CM=2 ![]() ������
������ ![]() =
= ![]() ��
�� ![]() =
= ![]() �ֱ����MN���ɵã�
�ֱ����MN���ɵã�
�����㾫����������Ҫ�����˶��κ��������ʵ����֪ʶ�㣬��Ҫ���������ԣ���a>0ʱ���Գ�����ߣ�y��x�������С���Գ����ұߣ�y��x���������a<0ʱ���Գ�����ߣ�y��x�������Գ����ұߣ�y��x�������С������ȷ�����⣮

 ����νӽ̲���ĩ���Ԥϰ�人������ϵ�д�
����νӽ̲���ĩ���Ԥϰ�人������ϵ�д� ������ҵ��ٳɳ����½������������ϵ�д�
������ҵ��ٳɳ����½������������ϵ�д�