��Ŀ����
����Ŀ��ij��˾Ϊһ�����͵��Ӳ�Ʒ�ڸó��е���Լ�����̣���֪ÿ����Ʒ�Ľ���Ϊ40Ԫ���ù�˾ÿ���������ֲ�Ʒ��������֧�����������ۣ��ܼ�100��Ԫ�������۹����е�֪����������y������������۵���x��Ԫ��֮����������ʾ�ĺ�����ϵ�����ҷ���y��x��һ�κ�����
���۵���x��Ԫ�� | 50 | 60 | 70 | 80 |
��������y������� | 5.5 | 5 | 4.5 | 4 |
��1����y��x�ĺ�����ϵʽ��
��2���ʣ������۵���xΪ��ֵʱ���ù�˾������������������ֵ��
����ע��������=�����۶�ܽ����۩�������֧��
��3������˾ϣ����������60��Ԫ����������ù�˾ȷ�����۵��۵ķ�Χ��
���𰸡���1��y=��![]() x+8����2����x=100ʱ���ù�˾���������ֵΪ80��Ԫ����3���ù�˾ȷ�����۵���x�ķ�Χ�ǣ�80��x��120��
x+8����2����x=100ʱ���ù�˾���������ֵΪ80��Ԫ����3���ù�˾ȷ�����۵���x�ķ�Χ�ǣ�80��x��120��
��������
�����������1�����ݱ��е���֪����������ô���ϵ����ȷ��ֱ�ߵĽ���ʽ���ɣ�
��2������������=��������������г�������ϵʽ�䷽��ȷ����ֵ��
��3�����������60�����Ӧ���Ա�����ֵ����ȷ�����۵��۵ķ�Χ��
�⣺��1����y=kx+b���ѣ�60��5������80��4������ã�![]() ��
��
��ã�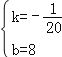 ��
��
�ʴ�Ϊ��y=��![]() x+8��
x+8��
��2���ù�˾������w=����![]() x+8����x��40����100=��
x+8����x��40����100=��![]() ��x��100��2+80��
��x��100��2+80��
��x=100ʱ���ù�˾���������ֵΪ80��Ԫ��
��3���⣺������ã���![]() ��x��100��2+80=60��
��x��100��2+80=60��
��ã�x1=80��x2=120��
�ʸù�˾ȷ�����۵���x�ķ�Χ�ǣ�80��x��120��
