题目内容
【题目】二次函数y=![]() x2-
x2-![]() x+6的图象与x轴相交于A,B两点(点A在点B的左边),与y轴交于点C.
x+6的图象与x轴相交于A,B两点(点A在点B的左边),与y轴交于点C.

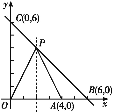
(1)求A,B,C三点的坐标;
(2)如果P(x,y)是线段BC上的动点,O为坐标原点,试求△POA的面积S与x之间的函数关系式,并写出自变量x的取值范围;
(3)在(2)的条件下,是否存在这样的点P,使得PO=PA?若存在,求出点P的坐标;若不存在,请说明理由.
【答案】(1)A(4,0),B(6,0),C(0,6).(2)S△POA=![]() ×4×(-x+6)=-2x+12,x的取值范围是0≤x<6.(3)存在这样的点P(2,4),使得OP=AP.
×4×(-x+6)=-2x+12,x的取值范围是0≤x<6.(3)存在这样的点P(2,4),使得OP=AP.
【解析】
(1)由图像与x轴相交是,y=0,可求出x的值,即可求出A点、B点的坐标,与y轴相交时x=0可求出y的值,即可得C点坐标;(2)根据B、C坐标可求出直线BC的一次函数解析式,根据三角形面积公式列出解析式即可;(3)由OP=AP可知P在OA的垂直平分线上,即可求出P点的横坐标,代入BC的解析式求出P点纵坐标即可判断是否存在.
(1)由题意,在y=![]() x2-
x2-![]() x+6中,
x+6中,
令y=0,
0=![]() x2-
x2-![]() x+6,
x+6,
解得x=4或6,
当x=0,y=6,
可得A(4,0),B(6,0),C(0,6).
(2)设直线BC的解析式为y=kx+b,
将B(6,0),C(0,6)代入上式,得
![]() 解得
解得![]()
所以y=-x+6,
根据题意得S△POA=![]() ×4×y,
×4×y,
所以S△POA=![]() ×4×(-x+6)=-2x+12,
×4×(-x+6)=-2x+12,
x的取值范围是0≤x<6.
(3)若PO=PA,
则点P在线段OA的垂直平分线上,
因为OA=4,
所以P点横坐标为2,代入直线BC解析式得
y=-x+6=-2+6=4,
所以P点坐标为(2,4),
所以存在这样的点P(2,4),使得OP=AP.

练习册系列答案
相关题目