Question

【题目】如图所示，已知直线、相交于，，射线从位置起始，绕点逆时针旋转，终边与始边形成的角度为.

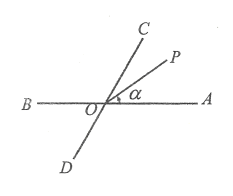
问题1：若逆时针旋转停止，则

（1）__________________时，平分；

（2）__________________时，；

（3）__________________时，；

问题2：若逆时针旋转的速度为每秒，在匀速旋转的同时，直线也从图的位置开始绕点逆时针匀速旋转，旋转速度为每秒，当完成旋转一周时，也同时停止旋转.设旋转时间为（）秒.

（1）旋转时间为多少时，射线与重合.请写出求解过程.

（2）观察旋转全过程，判断旋转时间为多少时，射线平分.请直接写出的值.（注：指大于且小于的角）

Answer 1

【答案】问题1：（1）（2）150°；（3）=40°或120°；问题2：（1）t=20秒；（2）t=秒.

【解析】

问题1：（1）根据和角平分线定义即可解答。

(2)由垂直定义知，∠POC=90°，因为，可得=∠POC+.

（3）=40°或90°。应分两种情况讨论：

②当射线OP在∠BOC内部时，根据即可解答；

问题2：（1）类似于行程问题中的追击问题，当射线与重合时，∠AOC=∠AOP

解：问题1：（1）因为，平分， ∠AOP= =30°；

（2）150°时，.

因为从OA开始，逆时针旋转停止，若满足，又因为，所以∠AOP=90°+60°=150°.

（3）=40°或120°。①当射线OP在∠AOC内部时，因为，，所以）∠APO= =40°；

②当射线OP在∠BOC内部时，如图：因为， ，所以∠APO=2 =120°；

问题2：（1）当旋转t秒时，∠AOP=8t，∠AOC=60°+5t，因为射线与重合，所以∠AOP=∠AOC，即8t=60°+5t，解得t=20，即t=20秒时，射线与重合.

（2）t秒时，∠AOC=60°+5t，∠AOP=8t，当射线平分时，∠AOP= ，即8t=（60°+5t），解得：t=，所以当t=秒时，射线平分.