题目内容
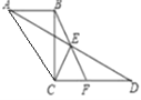
【题目】如图,AB∥CD,连接AD,点E是AD的中点,连接BE并延长交CD于F点.
(1)请说明△ABE≌△DFE的理由;
(2)连接CB,AC,若CB⊥CD,AC=CD,∠D=30°,CD=2,求BF的长.
【答案】(1)证明见解析;(2)BF=2
【解析】
利用三角形全等判定条件ASA进行判断.
利用30°所对直角边等于斜边的一半求出CE的长,再利用BF=2CE求出BF的长度.
证明:∵AB∥CD
∴∠BAE=∠EDF
∵点E是AD的中点
∴AE=ED
又∵∠AEB=∠FED
∴△ABE≌△DFE(ASA)
(2)∵AC=CD 且E为AD中点 ∴CE⊥AD
∵∠D=30°且CD=2 ∴CE=1
又∵CB⊥CD且BE=EF ∴BF=2CE
∴BF=2.

练习册系列答案
相关题目