题目内容
【题目】二次函数y=ax2+bx+c，自变量x与函数y的对应值如表：
x | … | ﹣5 | ﹣4 | ﹣3 | ﹣2 | ﹣1 | 0 | … |
y | … | 4 | 0 | ﹣2 | ﹣2 | 0 | 4 | … |
下列说法正确的是（ ）
A.抛物线的开口向下
B.当x＞﹣3时，y随x的增大而增大
C.二次函数的最小值是﹣2
D.抛物线的对称轴是x=﹣ 
【答案】D
【解析】解：将点（﹣4，0）、（﹣1，0）、（0，4）代入到二次函数y=ax2+bx+c中，得：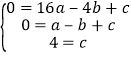 
，解得： 
，
∴二次函数的解析式为y=x2+5x+4．
A、a=1＞0，抛物线开口向上，A不正确；
B、﹣ 
=﹣ 
，当x≥﹣ 时，y随x的增大而增大，B不正确；
C、y=x2+5x+4= 
，二次函数的最小值是﹣ 
，C不正确；
D、﹣ =﹣ ，抛物线的对称轴是x=﹣ ，D正确．
故选D．
【考点精析】解答此题的关键在于理解二次函数的性质的相关知识，掌握增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小．
练习册系列答案
相关题目
【题目】我们在学完“平移、轴对称、旋转”三种图形的变化后，可以进行进一步研究，请根据示例图形，完成下表．
图形的变化 | 示例图形 | 与对应线段有关的结论 | 与对应点有关的结论 |
平移 |
| AA′=BB′ | |
轴对称 |
| ||
旋转 |
| AB=A′B′；对应线段AB和A′B′所在的直线相交所成的角与旋转角相等或互补． |
