题目内容
【题目】如图,在△ABC中,AB=AC,∠A=120 ![]() ,BC=6cm,AB的垂直平分线交BC于点M,交AB于点E,AC的垂直平分线交BC于点N,交AC于点F,则MN的长为( )
,BC=6cm,AB的垂直平分线交BC于点M,交AB于点E,AC的垂直平分线交BC于点N,交AC于点F,则MN的长为( )
A.1.5cm
B.2cm
C.2.5cm
D.3cm
【答案】B
【解析】连接AM、AN,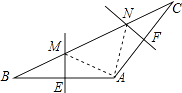
∵在△ABC中,AB=AC,∠A=120°,BC=6cm,
∴∠B=∠C=30°,
∵EM垂直平分AB,NF垂直平分AC,
∴BM=AM,CN=AN,
∴∠MAB=∠B=30°,∠NAC=∠C=30°,
∴∠AMN=∠B+∠MAB=60°,∠ANM=∠C+∠NAC=60°,
∴△AMN是等边三角形,
∴AM=MN=NC,
∴BM=MN=CN,
∵BM+MN+CN=BC=6cm,
∴MN=2cm ,
故答案为:B.
根据垂直平分线上的点到线段两端点的距离相等,因此连接AM、AN,得出BM=AM,CN=AN,再根据∠A=120 ° ,得出∠B=∠C=30°,根据等腰三角形的性质及三角形的外角性质易证得△AMN是等边三角形,得出AM=MN=NC,然后根据BC的长,可求出MN的长。

练习册系列答案
相关题目