题目内容
【题目】如图,![]() 和
和![]() 都是等边三角形,点
都是等边三角形,点![]() 在
在![]() 的延长线上.
的延长线上.

(1)找出图中一对全等三角形,并证明其全等;
(2)求![]() 的度数?若
的度数?若![]() ,
,![]() ,求
,求![]() 的长。
的长。
【答案】(1)△ABD≌△ACE,证明见解析;(2)60°,5
【解析】
(1)根据等边三角形的性质推出AB=AC,AD=AE,∠BAC=∠DAE=60°,根据SAS可证△ABD≌△ACE;
(2)根据全等三角形的性质推出∠ABD=∠ACE,根据∠BAC+∠ABD=∠ACE+∠BEC,推出∠BEC=∠BAC=60°即可.
(1)△ABD≌△ACE,证明如下,
∵△ABC和△ADE是等边三角形,
∴AB=AC,AD=AE, ∠BAC=∠DAE,
∴∠BAD=∠CAE,
∴△ABD≌△ACE.
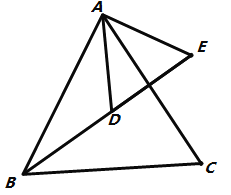
(2)如图,设AC与BE交于点O,
∵△ABD≌△ACE,
∴∠ABD=∠ACE,
∵∠AOB=∠EOC, ∠AOB+∠ABE+∠BAC=∠EOC+∠ACE+∠BEC,
∴∠BEC=∠BAC=60°,
即∠BEC =60°;
∵△ABD≌△ACE,
∴BD=CE=3,
∵△ADE是等边三角形,
∴DE=AE=2,
∴BE=BD+DE=3+2=5

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目