��Ŀ����
����Ŀ���ۺ���
��1����̽�����֡���ͼ�٣���һ��ֱ��������ֽƬ����B=60�㣬С������м���һ���ԡ�BΪ�ڽ���������ľ��Σ�������β������֣���������λ��DE��EF����ʱ�����õľ��ε������������ͨ��֤����֤������ȷ�ԣ����ó������ε���������ԭ����������ı�ֵΪ ��
��2������չӦ�á���ͼ�ڣ��ڡ�ABC�У�BC=a��BC���ϵĸ�AD=h������PQMN�Ķ���P��N�ֱ��ڱ�AB��AC�ϣ�����Q��M�ڱ�BC�ϣ������PQMN��������ֵΪ �� ���ú�a��h�Ĵ���ʽ��ʾ��
��3�������Ӧ�á���ͼ�ۣ���һ�顰ȱ�Ǿ��Ρ�ABCDE��AB=32��BC=40��AE=20��CD=16��С�����м�����һ��������ľ��Σ���BΪ���������ε��ڽǣ�����þ��ε������
��4����ʵ��Ӧ�á���ͼ�ܣ�����һ���ı��ε�ľ������ABCD��������AB=50cm��BC=108cm��CD=60cm����tanB=tanC= ![]() ��ľ����ʦ������������вó��˶���M��N�ڱ�BC����������ľ���PQMN����þ��ε������
��ľ����ʦ������������вó��˶���M��N�ڱ�BC����������ľ���PQMN����þ��ε������
���𰸡�
��1��![]()
��2��![]()
��3��
�⣺�⣺��ͼ1���ӳ�BA��DE���ڵ�F���ӳ�BC��ED���ڵ�G���ӳ�AE��CD���ڵ�H��ȡBF�е�I��FG���е�K��
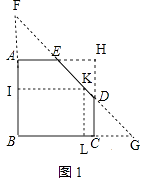
������֪�ı���ABCH�Ǿ��Σ�
��AB=32��BC=40��AE=20��CD=16��
��EH=20��DH=16��
��AE=EH��CD=DH��
�ڡ�AEF�͡�HED�У�
��  ��
��
���AEF�ա�HED��ASA����
��AF=DH=16��
ͬ����CDG�ա�HDE��
��CG=HE=20��
��BI= ![]() =24��
=24��
��BI=24��32��
����λ��IK�����˵����߶�AB��DE�ϣ�
����K��KL��BC�ڵ�L��
�ɣ�1��֪���ε�������Ϊ ![]() ��BGBF=
��BGBF= ![]() ����40+20������32+16��=720��
����40+20������32+16��=720��
�𣺸þ��ε����Ϊ720
��4��
��ͼ2���ӳ�BA��CD���ڵ�E������E��EH��BC�ڵ�H��
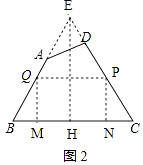
��tanB=tanC= ![]() ��
��
���B=��C��
��EB=EC��
��BC=108cm����EH��BC��
��BH=CH= ![]() BC=54cm��
BC=54cm��
��tanB= ![]() =
= ![]() ��
��
��EH= ![]() BH=
BH= ![]() ��54=72cm��
��54=72cm��
��Rt��BHE��BE= ![]() =90cm��
=90cm��
��AB=50cm��
��AE=40cm��
��BE���е�Q���߶�AB�ϣ�
��CD=60cm��
��ED=30cm��
��CE���е�P���߶�CD�ϣ�
����λ��PQ�����˵����߶�AB��CD�ϣ�
�ɡ���չӦ�á�֪������PQMN��������Ϊ ![]() BCEH=1944cm2��
BCEH=1944cm2��
�𣺸þ��ε����Ϊ1944cm2
���������⣺��1����̽�����֡�
��EF��EDΪ��ABC��λ�ߣ�
��ED��AB��EF��BC��EF= ![]() BC��ED=
BC��ED= ![]() AB��
AB��
�֡�B=90�㣬
���ı���FEDB�Ǿ��Σ�
�� ![]() =
= ![]() =
= 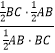 =
= ![]() ��
��
���Դ��ǣ� ![]() ��
��
�ơ���չӦ�á�
��PN��BC��
���APN�ס�ABC��
�� ![]() =
= ![]() ����
���� ![]() =
= ![]() ��
��
��PN=a�� ![]() PQ��
PQ��
��PQ=x��
��S����PQMN=PQPN=x��a�� ![]() x��=��
x��=�� ![]() x2+ax=��
x2+ax=�� ![]() ��x��
��x�� ![]() ��2+
��2+ ![]() ��
��
�൱PQ= ![]() ʱ��S����PQMN���ֵΪ
ʱ��S����PQMN���ֵΪ ![]() ��
��
���Դ��ǣ� ![]() ��
��
�����㾫����������Ҫ��������������λ�߶����;��ε����ʵ����֪ʶ�㣬��Ҫ�������������������е���߶ν��������ε���λ������������λ�߶����������ε���λ��ƽ���������εĵ����ߣ��ҵ��ڵ����ߵ�һ�룻���ε��ĸ��Ƕ���ֱ�ǣ����εĶԽ�����Ȳ�����ȷ�����⣮

 ���ɿ��õ�Ԫ������ĩר����100��ϵ�д�
���ɿ��õ�Ԫ������ĩר����100��ϵ�д�